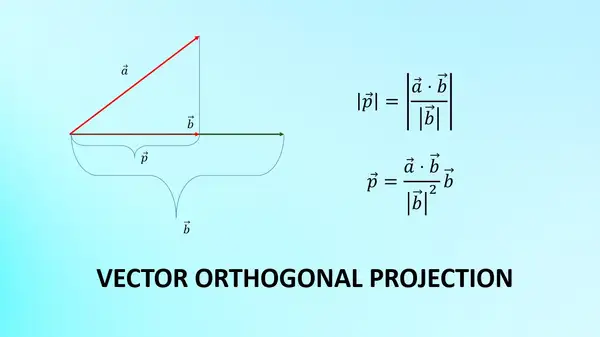
Orthogonal projection of a vector onto another vector, the result is a vector. Meanwhile, the length of an orthogonal vector projection of a vector onto another vector always has a positive real number/scalar value.
In this article we will discuss vector projections, especially orthogonal (perpendicular) vector projections.
Orthogonal projection of a vector onto another vector, the result is a vector. Meanwhile, the length of the projection of an orthogonal vector on another vector is always a positive real number/scalar.
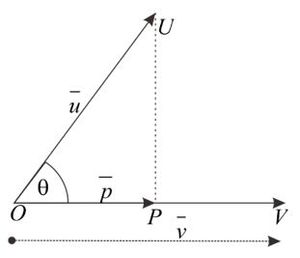The orthogonal projection of vector $\vec{u}$ on vector $\vec{v}$ can be denoted by ${\vec{u}}_{\vec{v}}$ or $\vec{p}$ and is defined by the following argument.
Proposition:
- Projeksi scalar orthogonal $\vec{u}$ falls on $\vec{v}$ adalah $$\left| \left| \vec{p}\right| \right|=\frac{\vec{u}\cdot\vec{v}}{\left| \vec{v}\right|}$$
- The projection of the vector $\vec{u}$ onto the vector $\vec{v}$ is the vector $${\vec{u}}_{\vec{v}}=\left( \frac{\vec{u } \cdot \vec{v}}{\left|. \vec{v} \right|^2} \right)\vec{v}\text{ atau } \vec{p}=\frac{\vec{u }}{\left| \vec{v} \right|} \left| \left| \vec{p} \right| \right|$$
- Panjang project vector $\vec{u}$ to vector $\vec{v}$ adalah $$ \lvert \vec{u}_{\vec{v}}\rvert=\left| \vec{u}\cdot e_{\vec{v}} \right| $$ dengan $e_{\vec{v}}$ adalah vector satuan ke arah $\vec{v}$ atau $\left| \vec{u}_{\vec{v}} \right|=\left| \frac{\vec{u}.\vec{v}}{\left| \vec{v} \right|} \right|$ .
Example 1:
Given $\vec{a}=2\widehat{i}-6\widehat{j}-3\widehat{k}$ and $\vec{b}=4\widehat{i}+2\widehat{j} -4\widehat{k}$. Determine:
- The length of the vector projection $\vec{a}$ on $\vec{b}$
- Orthogonal projection of vector $\vec{a}$ on $\vec{b}$
- Orthogonal projection of vector $\vec{b}$ on $\vec{a}$
Alternative Solutions:
The length of the vector projection $\vec{a}$ on $\vec{b}$ $$\begin{align*} \left| \vec{a}_{\vec{b}} \right|=\left| \frac{\vec{a}.\vec{b}}{\left| \vec{b} \right|} \right|&=\left| \frac{(2\widehat{i}-6\widehat{j}-3\widehat{k})\cdot (4\widehat{i}+2\widehat{j}-4\widehat{k})}{\sqrt{{{4}^{2}}+{{2}^{2}}+{{(-4)}^{2}}}} \right| \\ &=\left| \frac{(2)(4)+(-6)(2)+(-3)(-4)}{\sqrt{16+4+16}} \right| \\ &=\left| \frac{8-12+12}{\sqrt{36}} \right|=\left| \frac{8}{6} \right| \end{align*}$$ $ \therefore \left| \vec{a}_{\vec{b}} \right|=\frac{4}{3}$
Orthogonal projection of vector $\vec{a}$ on $\vec{b}$
$\vec{a}_{\vec{b}}=\left| \left| \vec{a}_{\vec{b}} \right| \right|\frac{\vec{b}}{\left| \vec{b} \right|}$, karena $\left| \vec{b} \right|=6$ dan $\left| \left| {{\vec{a}}_{\vec{b}}} \right| \right|=\frac{4}{3}$
$$\begin{align*} \vec{a}_{\vec{b}}&=\frac{4}{3}.\frac{4\widehat{i}+2\widehat{j}-4\widehat{k}}{6} \\ & =\frac{8}{9}\widehat{i}+\frac{4}{9}\widehat{j}-\frac{8}{9}\widehat{k} \end{align*}$$Orthogonal projection of vector $\vec{b}$ on $\vec{a}$
$$\begin{align*}\vec{b}_{\vec{a}}&=\left( \frac{\vec{b}\cdot \vec{a}}{{{\left| \vec{a} \right|}^{2}}} \right)\vec{a} \\ &=\frac{(4\widehat{i}+2\widehat{j}-4\widehat{k})\cdot (2\widehat{i}-6\widehat{j}-3\widehat{k})}{{{\left( \sqrt{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}} \right)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{(4)(2)+(2)(-6)+(-4)(-3)}{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{8}{49}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ \vec{b}_{\vec{a}}&=\frac{16}{49}\widehat{i}-\frac{48}{49}\widehat{j}-\frac{24}{49}\widehat{k})\end{align*}$$
example 2
Given the vectors $ \vec{u} = (-1,1,-4) $ and $ \vec{v} = ( 2, -1,3) $ . Determine the scalar projection and vector projection $ (2\vec{u} + 3\vec{v}) $
falls $ -2\vec{v} $!
Solution:
for example:
$ \vec{a} = (2\vec{u} + 3\vec{v}) = (-2,2,-8) + ( 6, -3,9) = (4, -1 , 1) $
$ \vec{b} = -2 \vec{v} = (-4, 2,-6) $
- Determine the scalar projection $ \vec{a} $ on $ \vec{b} $
$$\begin{align*}\text{Projective scalar } &= \frac{\vec{a}.\vec{b}}{|\vec{b}|} \\&= \frac{4 .(-4) + (-1). 2 + 1. (-6)}{\sqrt{(-4)^2 + 2^2 + (-6)^2} } \\&= \frac{-16 - 2 - 6}{\ sqrt{16 + 4 + 36 } } \\&= \frac{-24}{\sqrt{56} } \\&= \frac{-24}{56} \sqrt{56} \ \&= -\frac{3}{7} \sqrt{56}\end{align*}$$
$\therefore$ so the scalar projection is $ -\frac{3}{7} \sqrt{56} $. - Determine the projection of the vector $ \vec{a} $ on $ \vec{b} $
$$\begin{align*}\text{Proyeksi vector } &= \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2} \right) \vec{b}\\&= \left( \frac{-24}{(\sqrt{56})^2} \right) ( -4, 2,-6)\\&= \left( \frac{-24}{56} \right) ( -4, 2,-6)\\ &= \left( -\frac{3}{7} \right) ( -4, 2,-6)\\&= \left( \frac{12}{7}, -\frac{6}{7}, \frac{18}{7} \right)\end{align*}$$
$\therefore$ so, the vector projection is $ \left( \frac{12}{7}, -\frac{6}{7}, \frac{18}{7} \right) $.
Example 3
Diketahui vector $ \vec{p} = 2\vec{i}+\vec{j} +2\vec{k} $ dan $ \vec{q} = 3\vec{i} + b\vec{j} + \vec{k} $. If $ |\vec{r}| $ adalah panjang projeksi
vector $ \vec{q} $ on $ \vec{p} $ and $ |\vec{r}| = 4 $, then determine the value of $ b $!
Solution:
Given the vectors $ \vec{p} = (2, 1, 2) $ and $ \vec{q} = (3, b, 1) $ .
- Determining the value of $ b $ by orthogonal projection $ \vec{q} $ on $ \vec{p} $ :
$$\begin{align*}\text{Panjang proyeksi } &= \left| \frac{\vec{q}.\vec{p}}{|\vec{p}|} \right|\\|\vec{r}| &= \left| \frac{\vec{q}.\vec{p}}{|\vec{p}|} \right|\\4 &= \left| \frac{ 2.3 + 1.b + 2.1 }{ \sqrt{2^2 + 1^2 + 2^2 } } \right|\\4 &= \left| \frac{ b + 8 }{ \sqrt{9} } \right|\\4 &= \left| \frac{ b + 8 }{ 3 } \right| \\| b + 8 | &= 12 \\ b &= 4 \vee b = -20 \end{align*}$$
So, the possible values of $ b $ are $ b = -20 $ or $ b = 4 $.
Example 4
Determine the projection of the vector $ \vec{a} = (2,0,1) $ on the vector $ \vec{b} $ which is parallel and equal in length but in the opposite direction to
vector $ \vec{c} = (0, 2, -2 ) $ !
Solution:
Diketahui vector $ \vec{b} = - \vec{c} = -(0, 2, -2) = (0, -2, 2) $.
- Determine the projection of the vector $ \vec{a} $ on $ \vec{b} $ :
$$\begin{align*}\text{Proyeksi vector } &= \left( \frac{\vec{a}.\vec{b}}{|\vec{b}|^2} \right) \vec{b} \\&= \left( \frac{2.0 + 0. (-2) + 1.2}{(\sqrt{0^2 + (-2)^2 + 2^2 })^2 } \right) (0, -2, 2)\\&= \left( \frac{2}{(\sqrt{8 })^2 } \right) (0, -2, 2)\\ &= \left( \frac{2}{8 } \right) (0, -2, 2) \\&= \left( \frac{1}{4 } \right) (0, -2, 2)\\&= \left( 0, -\frac{1}{2} , \frac{1}{2} \right) \end{align*}$$
So, the resulting vector projection is $ \left( 0, -\frac{1}{2} , \frac{1}{2} \right) $.