A two-dimensional vector is a vector that has two elements, namely vertical (Y-axis) and horizontal (X-axis). Vectors in a flat plane (second dimension) are characterized by the X-axis and the Y-axis, which intersect at the center point O ( 0, 0)

Table Of Contents

A two-dimensional vector is a vector that has two elements, namely vertical (Y-axis) and horizontal (X-axis). Vectors in a plane (dimensional two) are characterized by an X-axis and a Y-axis, which intersect at the center point O (0, 0). Analytically, two-dimensional vectors can be presented according to their elements, namely:

Where x is the horizontal element. When $x > 0$ (positive) then x has a direction to the right and when $x < 0$ (negative) x has a direction to the left. Next, y is a vertical element. When $y > 0$ (positive) then the direction is up and if $y < 0$ (negative) the direction is down.

1. Vector Components, Column Vectors, and Row Vectors

Look at the vector in the following image 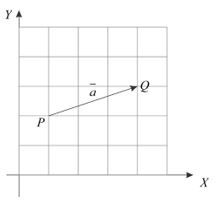Vector Columns In general, the vector $\vec{a}$ in the image above can be written in columns as follows $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3 \\ 1 \end{pmatrix}$$ Apart from column vectors, the vector $\vec{a}$ can also be written as a row vector as follows $$\vec{PQ}=\vec{a}=\begin{pmatrix} 3, 1\end{pmatrix}$$

$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$ is called a column vector and $\begin{pmatrix} 3, 1\end{pmatrix}$ is called a row vector. 3 and 1 are components of the Vector $\vec{a}$.

A vector depicted on a coordinate plane has a horizontal component (movement to the right/left) and a vertical component (movement up/down). Therefore, vectors can be presented in columns. Vector Component $$\vec{PQ}=\begin{pmatrix} \text{Horizontal component} \\ \text{vertical component}\end{pmatrix}$$

2. Position Vector

Position Vector is a vector that begins at the coordinate center $O(0,0)$ and ends at a point $(x,y)$. Consider any point $A(x_1, y_1)$ and point $B(x_2, y_2)$ in the following Cartesian coordinates. Position Vector In the figure above, the vector $\vec{a}$ represents a directed line segment from the origin $O(0, 0)$ to the point $A(x_1, y_1)$ or vector $\vec{OA}$. Therefore, the vector $\vec{a}$ can be written in column vector form
$\vec{OA}=\vec{a} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}$
The vector $\vec{b}$ represents a directed line segment from the origin $O(0, 0)$ to the point $B(x_2, y_2)$ or vector $\vec{OB}$. The vector $\vec{b}$ can be written as
$\vec{OB}=\vec{b} = \begin{pmatrix} x_2 \\ y_2 \end{pmatrix}$

Now consider the vector $\vec{AB}$. We get the vector $\vec{AB}$ by drawing a line from point A to point B. As previously studied, the vector $\vec{AB}$ can be expressed in the form of a geometric addition of vectors, namely $\vec{AB} =\vec{OB}-\vec{OA}$ so $$\begin{align*} \vec{AB}&=\vec{OB}-\vec{OA} \\ &=\vec{b}-\vec{a}\\ &= \begin{pmatrix}x_2\\y_2\end{pmatrix}-\begin{pmatrix}x_1\\y_1\end{pmatrix}\\ \vec{AB} &=\begin{pmatrix}x_2-x_1\\y_2-y_1\end{pmatrix} \end{align*}$$

3. Modulus or Vector Size

Modulus states the length or magnitude of the vector. Because the length or magnitude of a vector is always positive, the way to write the modulus uses the absolute sign 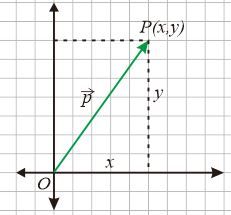$\left( \lvert {} \rvert \right)$. VectorLength If the coordinates of the point $P (x, y)$ are known then the length of the position vector $\vec{OP}=\begin{pmatrix} x \\ y \end{pmatrix}$ is formulated using the Pythagorean theorem or as follows $\lvert \vec{OP} \rvert=\sqrt{x^2+y^2}$.

Example 1
Given the vector $\vec{OQ}=\vec{q}=\begin{pmatrix}3 \\4 \end{pmatrix}$. Determine the Length of Vector $\vec{q}$

Alternative solutions
$$\begin{align*} & \lvert \vec{q} \rvert=\sqrt{3^2+4^2}\\ & \lvert \vec{q} \rvert=\sqrt{25}\\& \lvert \vec{q} \rvert=5\end{align*}$$ So, the length of vector $\vec{q}$ is 5 units

4. Unit vector

In the previous discussion, the unit vector of the vector $\vec{a}$ was formulated: $e_{\vec{a}}=\frac{\vec {a}}{\lvert \vec{a} \rvert}$ or $\widehat{a}=\frac{\vec{a}}{\ lvert \vec{a} \rvert}$

In a column Vector, if $\vec{a}=\begin{pmatrix} x \\ y \end{pmatrix},$ then $\widehat{a}=\frac{1}{\sqrt{x^2+y^2}}.\begin{pmatrix} x \\ y \end{pmatrix}$

5. Properties of Column Vector Operations

a. Vector Addition

Analytically, the addition of two vectors can be done as follows
$$\vec{a}+\vec{b} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix}+\begin{pmatrix} x_2 \\ y_2 \end{pmatrix}=\begin{pmatrix} x_1+x_2 \\ y_1+y_2 \end{pmatrix}$$ If the two vectors are known to flank a certain angle, then calculations can be used using the cosine rule formula as in trigonometry. ![Vector Addition](/images/k12/vector/vector addition.jpg) When the angle between $\vec{a}$ and $\vec{b}$ is $\theta$, then $$\begin{align*} {\lvert \vec{a}+\vec{b} \rvert}^2&=\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert \cos \theta \\ \lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert\lvert \vec{b} \rvert\cos \theta } \end{align*}$$

If vectors are presented in component form (in the Cartesian plane) then addition can be done by adding the components.

For example:
$\vec{a} = \begin{pmatrix} x_A \\ y_A \end{pmatrix}$ and $\vec{b}$ = $\begin{pmatrix} x_B \\ y_B \end{pmatrix}$ size $\vec{a}+\vec{b} = \begin{pmatrix} x_A+x_B \\ y_A+y_B \end{pmatrix}$

Example 2
Given the vector $\vec{a}=\begin{pmatrix} 2 \\ -3 \end{pmatrix}$ and the vector $\vec{b}=\begin{pmatrix} -4 \\ 3 \end {pmatrix}$. Determine the vector sum of $\vec{a}+\vec{b}$!
Alternative Solution
$\vec{a}+\vec{b}$ = $\begin{pmatrix} 2+(-4) \\ -3+3 \end{pmatrix}=\begin{pmatrix} -2 \\ 0 \end{pmatrix}$

Example 3
Given the length of the vector |$\vec{a}$| = 2 and the vector length is |$\vec{b}$| = 4, the angle between vectors $\vec{a}$ and $\vec{b}$ is $60^\circ$, then:

$$\begin{align*}\lvert \vec{a}+\vec{b} \rvert&=\sqrt{\lvert \vec{a} \rvert+\lvert \vec{b} \rvert+2\lvert \vec{a} \rvert \lvert \vec{b} \rvert \cos \theta } \\ &= \sqrt{2^2+4^2+2.2.4.\cos 60^\circ} \\ &= \sqrt{4+16+16.\tfrac{1}2} \\ &= \sqrt{28}\\ &=2\sqrt{7} \end{align*}$$

b. Vector Reduction

Analytically, if it is known Vector $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ and $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ then the reduction of two vectors can be formulated $\vec{a}- \vec{b}=\begin{pmatrix} a_1-b_1 \\ a_2-b_2 \end{pmatrix}$ Vector Subtraction Example 4 Given the vector $\vec{p}=\begin{pmatrix} 6 \\ -3 \end{pmatrix}$ and the vector $\vec{q}=\begin{pmatrix} -4 \\ 3 \end {pmatrix}$. Determine the vector of $\vec{p}-\vec{q}$!
Alternative Solution
$\vec{p}-\vec{q}$ = $\begin{pmatrix} 6-(-4) \\ -3-3 \end{pmatrix}=\begin{pmatrix} 10 \\ -6 \end{pmatrix}$

c. Scalar Multiplication with Vectors

Multiplying a scalar by a vector will produce a vector with the same direction. The vector $\vec{v}$ is parallel to the vector $\vec{u}$, written $\vec{v}//\vec{u}$ if:

  • If $k > 0$, then $\vec{v}$ is the direction of $\vec{u}$
  • If $k < 0$, then $\vec{v}$ is opposite to $\vec{u}$ Vector Multiplication

Analytically, if we know the vector $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \end{pmatrix}$ then $k.\vec{a}=\begin{pmatrix} k.a_1 \ \ k.a_2 \end{pmatrix}$, where $k$ is a constant. Example 5
Given $\vec{a} = \begin{pmatrix} -2 \\3 \\\end{pmatrix}$ and $\vec{b} = \begin{pmatrix}4 \\-2 \\\end{pmatrix}$ determine $3\vec{b} – \frac{1}{2}\vec{a}$! Alternative Solution
$$\begin{align*} 3\vec{b} – \frac{1}{2}\vec{a}&=3 \begin{pmatrix} -2 \\3 \\\end{pmatrix}-\frac{1}{2}\begin{pmatrix}4 \\-2 \\\end{pmatrix}\\ &= \begin{pmatrix} 3.(-2) \\3(3) \\\end{pmatrix}-\begin{pmatrix}\frac{1}{2}(4) \\\frac{1}{2}(-2) \\\end{pmatrix}\\&= \begin{pmatrix} -6 \\9 \\\end{pmatrix}-\begin{pmatrix}2 \\ -1 \\\end{pmatrix}\\&=\begin{pmatrix}-6-2 \\ 9-(-1) \\\end{pmatrix}\\&=\begin{pmatrix}-8 \\ 10 \\\end{pmatrix} \end{align*}$$ **Example 6**
Determine whether the points P(1, –2), Q(2, 1), and R(4, 7) are collinear (straight).
**Alternative Solutions:**
Points P, Q and R are said to be collinear (in line) if points P, Q and R lie on the same line. Points P, Q and R will lie on the same line if and only if the vectors representing the directed line segments of the points P, Q and R have the same base and are parallel.
The vectors $\vec{PQ}$ and $\vec{PR}$ have the same starting point.
Komponen vektor $\vec{PQ}=\vec{q}-\vec{p}=\begin{pmatrix}2 \\ 1 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}1 \\ 3 \end{pmatrix}$
Komponen vektor $\vec{PR}=\vec{r}-\vec{p}=\begin{pmatrix}4 \\ 7 \end{pmatrix}-\begin{pmatrix}1 \\ -2 \end{pmatrix}=\begin{pmatrix}3 \\ 9 \end{pmatrix}$

Two vectors are collinear if there is a number $k$ that satisfies $\vec{PR}=k.\vec{PQ}$ and both vectors have the same origin. $$\begin{align*} \vec{PR}&=\begin{pmatrix}3 \\ 9 \end{pmatrix}\\ &= 3\begin{pmatrix}1 \\ 3 \end{pmatrix}\\\vec{PR}&= 3\vec{PQ} \end{align*}$$ Because $\vec{PR}=3\vec{PQ}$ means that the vector $\vec{PQ}$ is parallel to the vector $\vec{PR}$ and both originate at point P. So, it can be concluded that point P, Q and R are points that are collinear (straight).

d. Similarity of two Vectors

Analytically, two Vectors $\vec{a}=\begin{pmatrix} a_1 \\ a_2 \\ \end{pmatrix}$ and $\vec{b}=\begin{pmatrix} b_1 \\ b_2 \end{pmatrix}$ are said to be equal if and only if $a_1=b_1$ and $a_2=b_2$

4. Standard Normal Base

Base definition

If each vector is 1 unit long and perpendicular to each other, then $\vec{v}_1,\vec{v}_2,\vec{v}_3,…,\vec{v}_n$ is called standard normal basis in $V$ space

Based on this definition, we can conclude that vectors:

  1. $\widehat{i}=\begin{pmatrix} 1 \\0 \\\end{pmatrix}$ and $\widehat{j}=\begin{pmatrix}0 \\1 \ \\end{pmatrix}$ is a standard normal basis in the vector space $R^2$ with $\widehat{i}$ and $\widehat{j}$ parallel to the X and Y axes respectively

  2. $\widehat{i}=\begin{pmatrix}1 \\0 \\0 \\\end{pmatrix},$ $\widehat{j}=\begin{pmatrix}0 \ \\1 \\0 \\\end{pmatrix}$ and $\widehat{k}=\begin{pmatrix}0 \\0 \\1 \\\end{ pmatrix}$ is a standard normal basis in the vector space $R^3$ with $\widehat{i}$, $\widehat{j}$ and $\widehat{k}$ parallel to the X, Y and Z axes.

Thus, if P is a point (x,y) and O(0,0), then the position vector $\vec{OP}$ can be written as a combination of two basis vectors $\vec{OP}=\vec{p}=\begin{pmatrix}x \\ y \\ \end{pmatrix}=x\begin{pmatrix} 1\\ 0\\ \end{pmatrix}+y\begin{pmatrix} 0\\ 1\\ \end{pmatrix}=x\widehat{i}+y\widehat{j}$

Example 7
Given the triangle OAB with vertices: O(0, 0), A(3, 1) and B(6, 5). $\vec{a}$ is the position vector of point 𝐴 and $\vec{b}$ is the position vector of point 𝐡. Express the vectors $\vec{a}$, $\vec{b}$ and $\vec{AB}$ in the form of basis vectors.
Alternative solution:
$\vec{a}=x_1\widehat{i}+y_1\widehat{j}=3\widehat{i}+\widehat{j}$
$\vec{b}=x_1\widehat{i}+y_1\widehat{j}=6\widehat{i}+5\widehat{j}$
$\vec{AB}=\vec{b}-\vec{a}=(6\widehat{i}+5\widehat{j})-(3\widehat{i}+\widehat{j})=3\widehat{i}+4\widehat{j}$

Exercise 3

  1. Look at the vector image on the side:
    Draw a vector Draw a vector:
    1. $3.\vec{u}$
    2. $-2.\vec{v}$
    3. $\vec{u} + \vec{v}$
    4. $2.\vec{u} – \vec{v}$
  2. If it is known that $\vec{u} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}$ and $\vec{v} = \begin{pmatrix}-4 \\ 1 \end{pmatrix}$ determine:
    1. $\vec{u}$
    2. $-3.\vec{v}$
    3. $3.\vec{u} + 2.\vec{v}$
    4. $2.\vec{v} – \vec{u}$
  3. Given the vectors $\vec{a} = \begin{pmatrix}2 \\-1 \\\end{pmatrix}$ and $\vec{b} = 2.\vec{a}$ , determine the vector $\vec{c} = \vec{a} + \vec{b}$
  4. Diketahui vector $\vec{a} = \begin{pmatrix}-2 \\ 4 \\ \end{pmatrix}$, $\vec{b} = \begin{pmatrix} x \\ \ y \\ \end{pmatrix}$ given c = $\begin{pmatrix}3 \\5 \\\end{pmatrix}$. Tentukan x given y if $\vec{c} = \vec{a} + \vec{b}$
  5. If the vector $\vec{m} = \begin{pmatrix}-8 \\ 4 \\ \end{pmatrix}$ and $\vec{n} = \begin{pmatrix}10 \\ -6 \\ \end{pmatrix}$ determine algebraically the vector of:
    1. $\frac{1}{2} \vec{m} – \frac{1}{2} \vec{n}$
    2. $\frac{1}{4} \vec{m} + \frac{1}{2} \vec{n}$
  6. Given $\vec{a} = \begin{pmatrix} -4 \\-2 \\\end{pmatrix}$ and $\vec{b} = \begin{pmatrix}1 \\ \\\end{pmatrix}$ determine $3\vec{b} – \frac{1}{2}\vec{a}$!
  7. If $\vec{a} = \begin{pmatrix}2 \\5 \\\end{pmatrix}$ and $\vec{b} = \begin{pmatrix}3 \\- 7 \\ \end{pmatrix}$ determine $2\vec{a} – \frac{1}{2}\vec{b}$!
  8. If $\vec{p} = \begin{pmatrix}5 \\-3 \\\end{pmatrix}$ and $\vec{q} = \begin{pmatrix}4 \\ -2 \\\end{pmatrix}$ determine $\frac{1}{2}\vec{b} – \frac{1}{2}\vec{q}$!
  9. If it is known that $\vec{p} = \begin{pmatrix}4 \\-6 \\ \end{pmatrix}$ and $\vec{q} = \begin{pmatrix} x \\ y \\ \end{pmatrix}$ determine x and y if $\vec{p} + \vec{q} = \begin{pmatrix} -2 \\ -3 \\ \end{pmatrix}$!
  10. If $\vec{a} = \begin{pmatrix}a_1 \\a_2 \\\end{pmatrix}$ and $\vec{b} = \begin{pmatrix}-9 \\ 2 \\\end{pmatrix}$ determine $a_1$ and $a_2$ if $\vec{a} – \vec{b} = \begin{pmatrix}4 \\7 \\\end {pmatrix}$!