determining the trigonometric ratio values of special angles 0°, 30°, 45°, 60°, 90° and solving them in everyday life
Trigonometry studies the relationship between sides and angles in a triangle and its properties and applications in various fields such as estimating the height of buildings or trees, horizontal distances to mountain peaks. towards the valley, and so on. This time we will discuss trigonometric ratios for special angles. To make it easier to understand this, first read Trigonometric Comparisons in Right Triangles↝ .
A special angle is an angle whose trigonometric ratio value can be determined directly without using a trigonometry chart or calculator.
The angles in question are angles whose magnitudes are $0^\circ, 30^\circ, 45^\circ, 60^\circ,$ and $90^\circ$.
How do you determine the trigonometric ratio values of these special angles? Here’s the explanation…
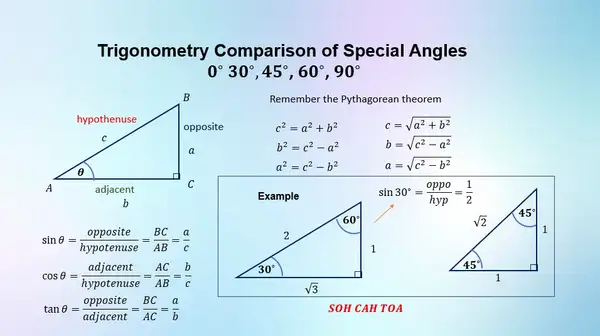
Trigonometric Comparison Values of Special Angles Quadrant I
We start from an equilateral triangle ABC with a side length of 2 units. Because the triangle is equilateral, the three sides are the same length and the three angles are also the same, namely 60°.
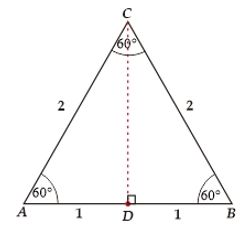 For example, if CD is the height and bisector of triangle ABC, then we can find line CD using Pythagorean theorem.
$$\begin{align*}CD&=\sqrt{BC^2-DB^2}\\&=\sqrt{2^2-1^2}\\&=\sqrt{4-1}\\CD&=\sqrt{3}\end{align*}$$
For example, if CD is the height and bisector of triangle ABC, then we can find line CD using Pythagorean theorem.
$$\begin{align*}CD&=\sqrt{BC^2-DB^2}\\&=\sqrt{2^2-1^2}\\&=\sqrt{4-1}\\CD&=\sqrt{3}\end{align*}$$
Thus, we can determine the trigonometric ratio values for angles 30° and 60°. Pay attention to triangle BCD and remember sindemi cossami tandesa...
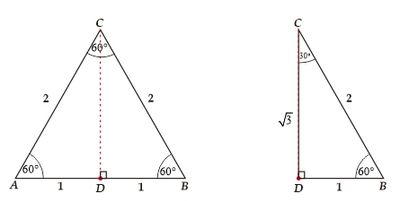
Trigonometry 30° Angles
The trigonometric comparison values for the 30° angle are as follows: $$\begin{align*}\sin 30^\circ&=\frac{de}{mi}=\frac{BD}{BC}=\frac{1}{2}\\\cos 30^\circ&=\frac{sa}{mi}=\frac{CD}{BC}=\frac{\sqrt3}{2}=\frac{1}{2}\sqrt{3}\\\tan 30^\circ&=\frac{de}{sa}=\frac{BD}{CD}=\frac{1}{\sqrt3}=\frac{1}{3}\sqrt{3}\end{align*}$$
Trigonometry 60° Angles
The trigonometric comparison values for angles of 60° are as follows: $$\begin{align*}\sin 60^\circ&=\frac{de}{mi}=\frac{BD}{BC}=\frac{1}{2}\\\cos 60^\circ&=\frac{sa}{mi}=\frac{BD}{BC}=\frac{\sqrt3}{2}=\frac{1}{2}\sqrt{3}\\\tan 60^\circ&=\frac{de}{sa}=\frac{BD}{BC}=\frac{1}{\sqrt3}=\frac{1}{3}\sqrt{3}\end{align*}$$
Trigonometry 45° Angles
Look at triangle ABC below.
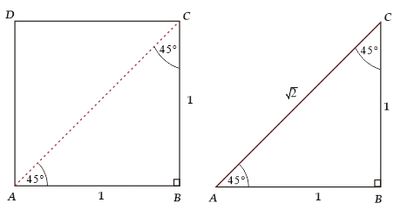
The trigonometric comparison values for the 45° angle are as follows: $$\begin{align*}\sin 45^\circ&=\frac{de}{mi}=\frac{AB}{AC}=\frac{1}{\sqrt2}=\frac12 \sqrt2\\\cos 45^\circ&=\frac{sa}{mi}=\frac{BC}{AC}=\frac{1}{\sqrt2}=\frac12 \sqrt2\\\tan 45^\circ&=\frac{de}{sa}=\frac{AB}{BC}=\frac{1}{1}=1\end{align*}$$
In full and in summary of the article above, the trigonometric comparison values of special angles in quadrant I are as follows:
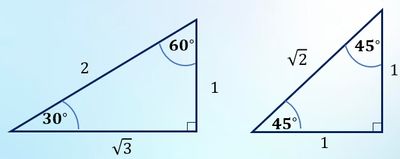
Table of Trigonometry Values
| $\theta$ | $\sin\theta$ | $\cos\theta$ | $\tan\theta$ |
|---|---|---|---|
| $0^\circ$ | 0 | 1 | 0 |
| $30^\circ$ | $\dfrac{1}{2}$ | $\dfrac{1}{2}\sqrt3$ | $\dfrac{1}{3}\sqrt3$ |
| $45^\circ$ | $\dfrac{1}{2}\sqrt2$ | $\dfrac{1}{2}\sqrt2$ | 1 |
| $60^\circ$ | $\dfrac{1}{2}\sqrt3$ | $\dfrac{1}{2}$ | $\sqrt3$ |
| $90^\circ$ | 1 | 0 | - |
Problems example
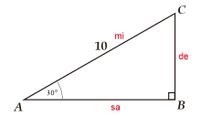
It is known that triangle ABC is right-angled at B, if the length of AC is 10 cm, and $\angle A = 30^\circ$. Find the lengths of AB and BC.
Solution ✍️
Is known: $\triangle ABC$ is right angled at B $\angle A=30^\circ$
$AC=10$ cm- Draw $\triangle ABC$

- find the length of AB To find the length of AB we can compare it using trigonometric ratios. AB is the side so we can use cosine $$\begin{align*} \cos A&=\frac{sa}{mi}\\ \cos 30^\circ&=\frac{AB}{AC}\\ \frac{\sqrt{3}}{2}&=\frac{AB}{10}\\ AB&=\frac{10\times \sqrt3}{2}\\ AB&=5\sqrt3\end{align*}$$
- find the length of BC using sine $$\begin{align*} \sin A&=\frac{de}{mi}\\ \sin 30^\circ&=\frac{BC}{AC}\\ \frac12&=\frac{BC}{10}\\ BC&=\frac{10\times 1}{2}\\ BC&=5\end{align*}$$
So, length $AB=5\sqrt3$ cm and $BC=5$
- Draw $\triangle ABC$
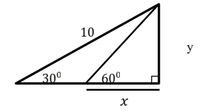
Calculate the value of 𝑥 in the following figure.

Solution ✍️
to determine the value of x we first determine the value of y- determine the value of y $$\begin{align*}\sin 30^\circ&=\frac{y}{10}\\ \frac{1}{2}&=\frac{y}{10}\\ y&=\frac{10\times 1}{2}\\ y&=5 \end{align*}$$
- determine the value of x $$\begin{align*}\tan 60^\circ&=\frac{y}{x}\\ \frac{\sqrt{3}}{1}&=\frac{5}{x}\\ x&=\frac{5\times 1}{\sqrt{3}}\\ x&=\frac{5}{3}\sqrt{3} \end{align*}$$
So, the value of x is $\frac{5}{3}\sqrt{3}$.
Application of Trigonometry in Everyday Life
There are many applications of trigonometry in everyday life. Trigonometric comparisons can be used to solve contextual problems related to observation angles, navigation, astronomy, civil engineering, measuring the height of an object, or to determine the distance to an object.
Some of the skills you need to have to improve your problem-solving abilities are:
- Understand the question Understand the question or problem given
- Choose a solution approach or strategy After understanding the problem, choose a formula/method for solving
- Finishing the model After choosing a solution strategy, carry out arithmetic operations or algebraic operations correctly to get a solution to the given problem
- Interpret the solution After the solution or completion of the mathematical model is obtained, then check the feasibility or correctness of the answer or the plausibility of the answer
To better understand, consider the following example:
Problems example
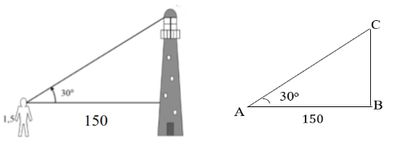
A tower is 150 meters from Andi, whose height is 150 cm. If Andi looks at the top of the tower using a clinometer, the elevation angle (the angle formed by the horizontal direction with the observer’s eye looking upwards) is $30^\circ$, determine the height of the tower.
Solution ✍️
understand the problem Is known : Elevation angle = $30^\circ$ Andi’s distance from the tower = 150 meters The distance between Andi’s eyes and the ground = 150 cm Wanted: tree height
Sketch of Andi’s position with the tower:

Choose a solution approach or strategy The relevant concept in the problem above is trigonometric ratios. For example, AB is the distance between the tower and Andi, and BC is the tower height minus Andi’s height. $$\tan A=\frac{de}{sa}=\frac{BC}{AB}$$
Finishing the model (finding the length of BC) $$\begin{align*} \tan A&=\frac{BC}{AB}\\ \tan 30^\circ&=\frac{BC}{150}\\\frac{\sqrt{3}}{3}&=\frac{BC}{150}\\ BC&=\frac{150\times \sqrt{3}}{3}\\ BC&=50\sqrt{3}\end{align*}$$
Interpret the solution $$\begin{align*}\text{Tower height} &= BC + \text{Andi’s height}\\ &= 50\sqrt{3} + 1.5 \\ & \approx 86.602 + 1 .5 \\ &\approx 88.102\end{align*}$$ So, the height of the tower is $(50\sqrt{3} + 1.5)$ m or around 88.102 m.
Thus the article about [Comparison of Trigonometry Special Angles](/comparison-trigonometry-special angles) may be useful.