The Sine Rule functions to connect the sides and angles of a triangle. The Cosine Rule is to connect three sides to one angle
The Sine Rule is an important rule that functions to connect the sides and angles of a triangle. Meanwhile, the Cosine rule is to connect three sides to one corner. The Sine Rule can be used in any triangle with known sides and opposite angles. The Cosine Rule is used to explain the relationship between the Cosine value and the square of the side length at one corner of a triangle.
Trigonometry cannot be separated from triangles, so this time we will study the sine rule and the cosine rule. We can find the angles and sides of a triangle using this rule. As explained above. To understand better, first study the material Trigonometric Comparisons in Right Triangles↝ , [Trigonometric Comparisons of Special Angles](/trigonometry-comparison-special angles), and also Trigonometry Comparison Values in Various Quadrants↝ .
1. Rule of Sines
The use of the sine rule applies to triangles, including right triangles to arbitrary triangles. Consider the following $\triangle ABC$.
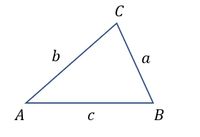From the picture above, the sine rule applies, namely:
$$\begin{align*} \frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C} \end{align*} $$
atau $$\begin{align*} \frac{\sin \angle A }{a} = \frac{\sin \angle B}{b} = \frac{\sin \angle C}{c} \end{align*} $$
Proof of the sine rule formula
Look at the following image.
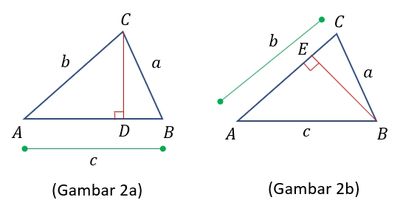
Gambar (2a),
- From $\triangle ADC$, $$ \begin{align}\sin A = \frac{CD}{AC} \nonumber \\ \rightarrow CD = AC \sin A \nonumber \\ \rightarrow CD_1 = b \sin A \end{align}$$
- From $\triangle BDC$, $$ \begin{align}\sin B = \frac{CD}{BC} \nonumber \\ \rightarrow CD = BC \sin B \nonumber \\ \rightarrow CD_2 = a \sin B \end{align}$$
- From equations (1) and (2) or the length of CD is obtained, $$ \begin{align}CD_1 = CD_2 \nonumber \\ \rightarrow b \sin A = a \sin B \nonumber \\ \rightarrow \frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} \end{align}$$
From figure (2b),
- From $\triangle AEB $, $$ \begin{align} \sin A = \frac{EB}{AB} \nonumber \\ \rightarrow EB = AB \sin A \nonumber \\ \rightarrow EB_1 = c \sin A \end{align}$$
- From $\triangle CEB$, $$ \begin{align} \sin C = \frac{EB}{CB} \nonumber \\ \rightarrow EB = CB \sin C \nonumber \\ \rightarrow EB_2 = a \sin C \end{align}$$
- From equations (4) and (5) or the length of EB is obtained, $$ \begin{align} EB_1 = EB_2 \nonumber \\ \rightarrow c \sin A = a \sin C \nonumber \\ \rightarrow \frac{a}{\sin \angle A} = \frac{c}{\sin \angle C} \end{align}$$
From equation (3) and equation (6) we get : $$ \frac{a}{\sin \angle A} = \frac{b}{\sin \angle B} = \frac{c}{\sin \angle C} $$ So, the sine rule formula is proven.
Example of the Sine Rule
1). Determine the length of AC in the following triangle!
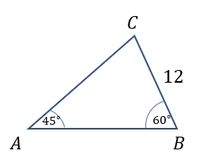
Solution ✍️
We use angles A and B for the sine rule: $$ \begin{align*} \frac{AC}{\sin B} &= \frac{BC}{\sin A} \\ \leftrightarrow \frac{AC}{\sin 60^\circ} &= \frac{12}{\sin 45^\circ} \\ \leftrightarrow \frac{AC}{\frac{1}{2}\sqrt{3}} &= \frac{12}{\frac{1}{2}\sqrt{2}} \\ \leftrightarrow \frac{AC}{\sqrt{3}} &= \frac{12}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{3}}}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{3}}}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}} \\ \leftrightarrow AC &= \frac{12{\sqrt{6}}}{2} \\ \leftrightarrow AC &= 6\sqrt{6} \end{align*} $$So, length $ AC = 6 \sqrt{6} $ . 😄
2). Given a triangle $KLM$ with side lengths $ML= 9$ cm and $KL = 12$ cm. Angle $M = 42^\circ$. Determine the measure of angle K! (use that $\sin 42^\circ = 0.669$ and $\cos 42^\circ = 0.743$)
Solution ✍️
If there are 2 sides with 1 angle that are opposite each other, then use the sine rule
$$\frac{KL}{\sin M}=\frac{ML}{\sin K}$$
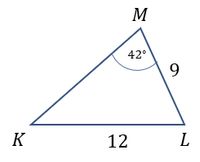
$$\begin{align*}\frac{KL}{\sin M}=\frac{ML}{\sin K}\\ \leftrightarrow \frac{12}{\sin 42^\circ}=\frac{9}{\sin K}\\ \leftrightarrow \frac{12}{0,669}=\frac{9}{\sin K}\\ \leftrightarrow \sin K=\frac{9\times0,669}{12}\\ \leftrightarrow \sin K \approx 0.50175\\ \leftrightarrow \ K \approx \arcsin{0.50175}\\ \leftrightarrow \ K \approx 30,1^\circ \end{align*}$$
So the measure of angle K is $30.1^\circ$
2. Cosine Rule
The law of cosines is a theorem used to determine the length of the front side of an angle by using the relationship between the two lengths of the flanks of the angle and its cosine value.
Consider the following $\triangle ABC$.
From the picture above, the sine rule applies, namely:
$$\begin{align*} a^2=b^2+c^2-2bc\cos A \\ b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C \end{align*} $$
or to determine the angle use the formula
$$\begin{align*} \cos A=\frac{b^2+c^2-a^2}{2bc}\\ \cos B=\frac{a^2+c^2-b^2}{2ac} \\ \cos C=\frac{a^2+b^2-c^2}{2ab} \end{align*} $$
Proof of the sine rule formula
Look at the following image.
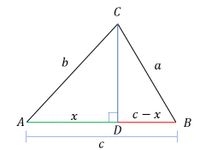
Consider triangle BCD where CD is perpendicular to BD. So by using the Pythagorean Theorem it is obtained that: $$\begin{align*}CD^2=BC^2-BD^2 \\ \Rightarrow CD^2=a^2-(c-x)^2 \tag{1} \end{align*}$$
Consider triangle ACD where CD is perpendicular to AD. So by using the Pythagorean Theorem it is obtained that: $$\begin{align*}CD^2=AC^2-BD^2 \\ \Rightarrow CD^2=b^2-x^2 \tag{2} \end{align*}$$
Remember again that: $$ \begin{align*}\cos A=\frac{AD}{AC}\\ \Rightarrow \cos A=\frac{x}{b} \\ \Rightarrow b =x \cos A \tag{3} \end{align*}$$
Based on Press. (1) and (2) then $$\begin{align*}CD^2&=CD^2 \\ \Rightarrow a^2-(c-x)^2&=b^2-x^2 \\ \Rightarrow a^2-(c^2-2cx+x^2)&=b^2-x^2 \\ \Rightarrow a^2-c^2+2cx-x^2&=b^2-x^2 \\ \Rightarrow a^2&=b^2+c^2-2cx \tag{4} \end{align*}$$
Substitute Press. (3) to Eq. (4) $$\begin{align*} a^2&=b^2+c^2-2cx \\ \Rightarrow a^2&=b^2+c^2-2cb \cos A \\ \Rightarrow a^2&=b^2+c^2-2bc \cos A \end{align*}$$
In the same way as above, by making a high line from each of the other corner points, namely AC and BC, you will get the cosine rule for the other sides as follows: $$b^2=a^2+c^2-2ac\cos B \\ c^2=a^2+b^2-2ab\cos C$$
So, the cosine rule formula is proven.
Example of the Cosine Rule
1). Determine the length of AB in the following triangle!
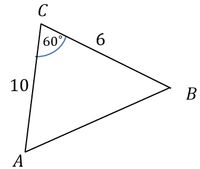
Solution ✍️
Based on the cosine rule: $$ \begin{align*} AB^2&=AC^2+BC^2-2.AC.BC \cos C \\ AB^2&=10^2+6^2-(2)(10)(6) \cos 60\degree \\ AB^2&=100+36-120. \frac{1}{2} \\ AB^2&=100+36-60 \\ AB^2&=76 \\ AB&=\sqrt{76} \\ AB&=\sqrt{4}\times\sqrt{19} \\ AB&=2\sqrt{19}\end{align*} $$
So, length $ AB = 2 \sqrt{19} $ . 😄
2). Given that triangle ABC has length $AB=12$ cm, $AC=8$ cm, and angle size $A=30\degree$. Then determine the length of side BC?
Solution ✍️
If 1 angle is enclosed by 2 sides, use the cosine rule
$$a^2=b^2+c^2-2bc\cos A$$
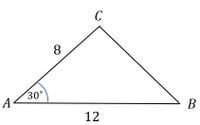
$$ \begin{align*} BC^2&=AB^2+AC^2-2.AB.AC \cos A \\ BC^2&=12^2+8^2-(2)(12) (8) \cos 30\degrees \\ BC^2&=144+64-192. \frac{1}{2}\sqrt{3} \\ BC^2&=208-96\sqrt{3} \\ BC&=\sqrt{208-96\sqrt{3}}\end{ align*} $$
So, length $ BC = \sqrt{208-96\sqrt{3}} $ . 😄