Learn how to easily perform matrix multiplication operations. Complete with example questions and step-by-step explanations. Merdeka Curriculum Phase F
Matrix multiplication is one of the basic operations in algebra that you learn in class XI Phase F of the Independent Curriculum. This operation has two main types, namely scalar multiplication with a matrix and matrix multiplication with a matrix. Each type of multiplication has different rules and properties.
Study Buddy! Before continuing, make sure you have understood and studied Matrix Concepts and Matrix Types↝ , as well as Matrix Transpose and Similarities↝ and Matrix Addition and Subtraction Operations↝ .
Scalar Multiplication with Matrices
Scalar multiplication with a matrix is the operation of multiplying each element in a matrix by a constant (scalar).
Definition:
Suppose A is a matrix of size m x n and k is a scalar. Then the multiplication of the scalar k with the matrix A is denoted by cA and is defined as:
$$kA = \begin{bmatrix}k.a_{11} & k.a_{12} & \cdots & k.a_{1n}\\ k.a_{21} & k.a_{22} & \cdots & k.a_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ k.a_{m1} & k.a_{m2} & \cdots & k.a_{mn} \end{bmatrix}$$
Example:
Given that the matrix $A = \begin{bmatrix} 2 & -1\\ 3 & 4 \end{bmatrix}$. Calculate the result of $3A$!
Solution ✍️
scalar multiplication of 3 with matrix A is: $$\begin{align*}3A &= 3 \begin{bmatrix}2 & -1\\3 & 4\end{bmatrix}\\&= \begin{bmatrix}3\times 2 & 3\times -1\\3\times3 & 3\times 4\end{bmatrix}\\&= \begin{bmatrix}6 & -3\\9 & 12\end{bmatrix}\end{align*}$$
Multiplication of Matrix by Matrix
Multiplication of matrix by matrix has special conditions, namely the number of columns of the first matrix must be the same as the number of rows of the second matrix.
Definition:
Suppose A is a matrix of size m x n and B is a matrix of size n x p. Then the multiplication of matrix A with matrix B is denoted by AB and is defined as:
$$(AB)_{ij} = \sum_{k=1}^{n} a_{ik}b_{kj}$$
where:
- $(AB)_{ij}$ is the element in the ith row and jth column of the multiplication matrix
- *$a_{ik}$* is the element in the ith row and kth column of matrix A
- *$b_{kj}$* is the element in the kth row and jth column of matrix B
Notes Multiplication of two matrices is done by multiplying each row of the first matrix by each column of the second matrix, then adding them to the same row.
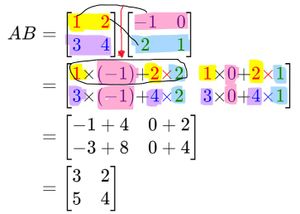
Example:
Given the matrix $A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} -1 & 0\\ 2 & 1 \end{bmatrix}$. Determine the result of the matrix multiplication $A\times B$!
Solution ✍️
Multiplication of matrix A with matrix B is:
$$\begin{align*}AB &= \begin{bmatrix} \color{red}{1} & \color{red}{2}\\ \color{blue}{3} & \color{blue}{4} \end{bmatrix} \begin{bmatrix} \color{purple}{-1} & \color{purple}{0}\\ \color{green}{2} & \color{green}{1} \end{bmatrix}\\ &= \begin{bmatrix} \color{red}{1} \color{black}{\times} \color{purple}{(-1)} \color{black}{+}\color{red}{2}{\times} \color{green}{2} & \color{red}{1} \color{black}{\times} \color{purple}{0} \color{black}{+}\color{red}{2}{\times} \color{green}{1}\\ \color{blue}{3}\color{black}{\times} \color{purple}{(-1)} \color{black}{+}\color{blue}{4}{\times} \color{green}{2} & \color{blue}{3} \color{black}{\times} \color{purple}{0} \color{black}{+}\color{blue}{4}{\times} \color{green}{1} \end{bmatrix}\\&= \begin{bmatrix} -1+4 & 0+2\\ -3+8 & 0+4 \end{bmatrix}\\ &= \begin{bmatrix} 3 & 2\\ 5 & 4 \end{bmatrix} \end{align*}$$
Properties of Matrix Multiplication
Matrix multiplication has several properties that need to be considered, but not all properties of real number multiplication apply to matrix multiplication. Following are some important properties of matrix multiplication:
Occurring Properties
Distributive of Addition:
- $A(B + C) = AB + AC$
- $(A + B)C = AC + BC$
Associative:
- $(AB)C = A(BC)$
Identity:
- $AI = IA = A$, where $I$ is the identity matrix.
Multiplication with Scalars:
- $c(AB) = (cA)B = A(cB)$, where $c$ is a scalar.
Properties that do not apply
- Commutative:
- $AB ≠ BA$ in general. This means that the order of matrix multiplication is very important and can produce different results.
Example of Matrix Multiplication Questions
Example Problem 1: Simple Multiplication
Given that matrices A and B are as follows:
$A = \begin{bmatrix} 2 & 1 \\-1 & 3\end{bmatrix}, B = \begin{bmatrix}4 & 0\\2 & -1\end{bmatrix} $
Determine the product of AB.
Solution ✍️
$$\begin{align*} AB &= \begin{bmatrix} 2 & 1\\ -1 & 3 \end{bmatrix} \begin{bmatrix} 4 & 0\\ 2 & -1 \end{bmatrix}\\ &= \begin{bmatrix} (2\cdot4)+(1\cdot2) & (2\cdot0)+(1\cdot-1)\\ (-1\cdot4)+(3\cdot2) & (-1\cdot0)+(3\cdot-1) \end{bmatrix}\\ &= \begin{bmatrix} 10 & -1\\ 2 & -3 \end{bmatrix} \end{align*}$$
Example Problem 2: Multiplication with Identity Matrix
The matrix C is known as follows:
$$ C = \begin{bmatrix} 3 & -2\\ 1 & 5 \end{bmatrix} $$
Determine the product $C\cdot I$, where I is the identity matrix of order 2x2.
Solution ✍️
The identity matrix of order 2x2 is:
$$ I = \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} $$
For,
$$\begin{align*} C \cdot I &= \begin{bmatrix} 3 & -2\\ 1 & 5 \end{bmatrix} \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \\ &= \begin{bmatrix} 3 & -2\\ 1 & 5 \end{bmatrix} \end{align*}$$
Example Problem 3: Multiplication with Scalars
Given the matrix $ D = \begin{bmatrix} -1 & 2\\ 4 & 0 \end{bmatrix} $. Determine the results of 3D.
Solution ✍️
To multiply a matrix by a scalar, we multiply each element of the matrix by the scalar:
$$ 3D = 3 \begin{bmatrix} -1 & 2\\ 4 & 0 \end{bmatrix} = \begin{bmatrix} -3 & 6\\ 12 & 0 \end{bmatrix} $$
Sample Question 4: Application Questions
A shop sells two types of goods, A and B. The profit per unit of good A is IDR 5,000.00 and good B is IDR 8,000.00. In the first week, the shop sold 100 units of item A and 150 units of item B. In the second week, the shop sold 120 units of item A and 180 units of item B.
a. Express the sales for both weeks in matrix form. b. Calculate the total profit for each week.
Discussion:
a. Sales matrix:
$$ \text{Week 1} = \begin{bmatrix} 100 \\ 150 \end{bmatrix}, \quad \text{Week 2} = \begin{bmatrix} 120 \\ 180 \end{bmatrix} $$
Price matrix per unit:
$$ \text{Price} = \begin{bmatrix} 5000 & 8000 \end{bmatrix} $$
b. Total profit:
- Week 1: $$\begin{align*}\text{Week 1 Profit} &= \begin{bmatrix} 5000 & 8000 \end{bmatrix} \begin{bmatrix} 100\\ 150 \end{bmatrix} \\ &= Rp. 1,700,000 \end{align*}$$
- Week 2: $$\begin{align*} \text{Week 2 Profits} &= \begin{bmatrix}5000 & 8000 \end{bmatrix} \begin{bmatrix} 120\\ 180 \end{bmatrix}\\ &= Rp. 2,040,000 \end{align*} $$
