What is a matrix? This time, we will discuss the concept of a matrix including its meaning and types which are studied in class XI Phase F. Listen carefully, OK!
Hi Sinmath friends, this time we will learn about the concept of matrices and also their types. A matrix in mathematics is a rectangular arrangement of numbers arranged in rows and columns. The matrix will be studied in class XI or phase F in the Independent Curriculum. The hope is that you can express the data in matrix form.
Matrices are used in solving various mathematical problems, for example: to find solutions to problems of linear equations, linear transformations. As an initial overview of the matrix, now try to look at the following description.
It is known that the entrance ticket price for a museum can be expressed as the following table:

This data can be presented again without having to be in a table, by removing the row heads and column heads as follows:
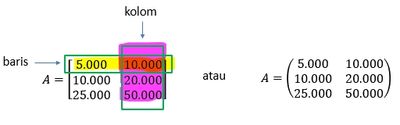
This writing form shows that there are 3 rows and 2 columns. The order of the numbers is the same as in the table. only the row and column information are removed. Then, the numbers are given in brackets on the right and left sides. In Mathematics, this shape is called a matrix.
Understanding Matrix
A matrix is an array of square or rectangular numbers arranged according to rows and columns, and placed in normal brackets or square brackets. Well, these brackets can be standard brackets “( )” or square brackets “[ ]” , yes
Matrices are named using capital letters, such as $A, B,$ and $C$.
General form of Matrix
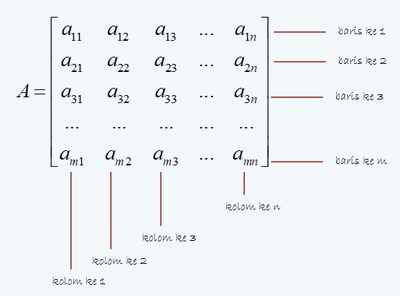 In the matrix form, the following things can be seen.
In the matrix form, the following things can be seen.
- The number of rows and columns of the matrix $A$ are m and n respectively.
- $a_{11}, a_{12}, a_{13}, …, a_{mn}$ are called the elements of matrix A, $a_{mn}$ = element $A$ in $m$th row, $n$th column.
The rows and columns are named sequentially, yes. So, row 1 starts from the top, descending in order. Meanwhile, the 1st column starts from left to right.
Matrix Order and Elements
Order or size of a matrix is determined by the number of rows and columns.
Generally applicable:
If matrix $A$ has $m$ rows and $n$ columns then matrix $A$ has order $m × n$ or the order of matrix A is $m × n$, written:
$A_{m×n}$ (read: ”A m times n”).
Each number contained in the matrix is called a matrix element. If a matrix is denoted with a capital letter, then the matrix elements are denoted with a lower case letter and are given an index that states the location of the rows and columns.
For example, matrix A
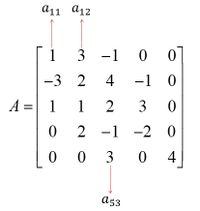
In the matrix A above, the number of rows is 5 and the number of columns is also 5, so the order is $5 \times 5$, or we can write $A_{5×5}$. Then, the elements of matrix A can be denoted by $a_{mn}$, which represents the element of matrix $A$ in the mth row and mth column.
For the elements, we take for example $a_{11}$, $a_{12}$, and $a_{53}$, as in the picture.
- $a_{11}$ represents the element of matrix A in the 1st row, the 1st column, the value is 1.
- $a_{12}$ represents the element of matrix A in the 1st row, the 2nd column, the value is 3.
- $a_{53}$ represents the element of matrix A in the 5th row, 3rd column, the value is 3.
Types of Matrices
Apart from having sizes (orders), matrices are also divided into several shapes that have special properties. So, some special types of matrices that you need to know include the following:
1. Row Matrix
A row matrix is a matrix that has only one row and the number of columns $n$, has the order $1 \times n$
Example: $$𝑃_{1\times3}= \begin{pmatrix}1 \\ 2 \\ -3\end{pmatrix}$$
2. Matrix Column
Column Matrix is a matrix that has only one column and m number of rows, has order m x 1
example: $$𝑃_{3\times1}= \begin{bmatrix}1 & 2 & -3\end{bmatrix}$$
3. Rectangular Matrix
A rectangular matrix is a matrix where the number of rows is not the same as the number of columns, has the order m x n
Example: $$R_{3\times2}= \begin{bmatrix}1 & 2 & -3 \\ -2 & 0 &2\end{bmatrix}$$
4. Square Matrix
Square Matrix or Square Matrix, namely a matrix that has the same number of rows as the number of columns, has order n x n Example: $$S_{3\times3}= \begin{bmatrix}1 & 2 & -3 \\ -2 & 0 &2 \\ -1 & 0 &3\end{bmatrix}$$
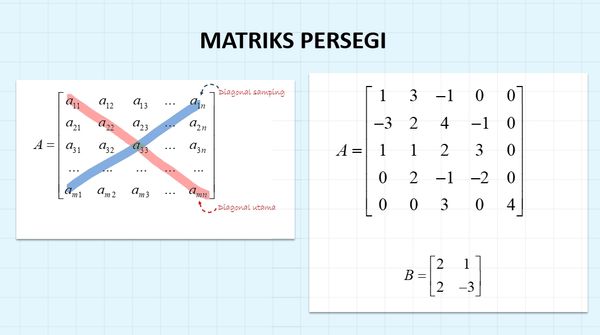
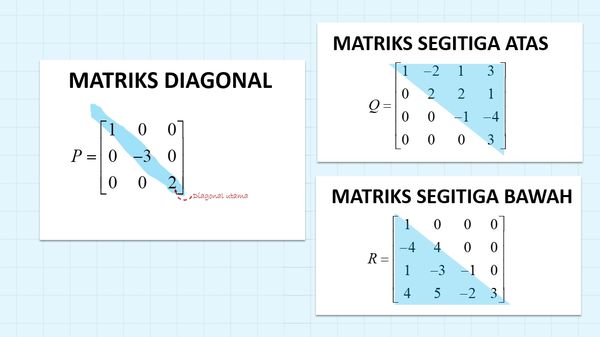
5. Diagonal Matrix
Diagonal Matrix, namely a square matrix of order n x n, with all elements outside the main diagonal having a value of zero
6. Upper Triangular Matrix
Upper Triangular Matrix, which is an n x n square matrix, and all elements below the main diagonal are zero
7. Lower Triangular Matrix
Lower Triangular Matrix, which is an n x n square matrix, and all elements above the main diagonal are zero
8 Identity Matrix
Identity matrix (unit matrix), namely a diagonal matrix with order n x n, and all elements on the main diagonal have a value of one, denoted by the letter “I”
Example: $$I= \begin{bmatrix}1 & 0 & 0 \\ 0 & 1 &0 \\ 0 & 0 &1\end{bmatrix}$$ The main diagonal element has a value of 1
9. Zero Matrix
Zero Matrix, namely a matrix of order m x n with all its elements having a value of zero Example: $$S_{3\times2}= \begin{bmatrix}0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}$$
How about it, guys, do you understand the concept of matrices? Actually, the matrix is an easy material, you know, it’s fun! This matrix can be used to quickly solve systems of equations that have more than two variables. Instead you have to use the substitution or elimination method. So, it is very important to understand this material.
As an exercise to further improve your understanding of the matrix, please look for 3 real problems in your daily life, then create:
- Form the matrix
- Order or size of the matrix
