Translation in Geometric Transformations is class xi mathematics material that you must study, let's look at the definition, example questions, and how to determine the image below
Sinmat Friends! Did you know that many activities or events in our daily lives are related to geometric transformations? What is Geometric Transformation? Geometric transformation is a change in the position and size of an object (point, line, curve, plane) and can be expressed in images and matrices. You will usually learn about geometric transformations in mathematics subjects in class XI.
Some of the things you will learn in this geometric transformation include Translation (Shift), Reflection (Mirror), Rotation (Spinning), and Dilation (Scaling).
- Translation is a transformation that moves points in a plane by the same direction and distance.
- Reflection is a transformation that moves each point on a plane using mirror image properties of the points to be moved. Deep mirror field geometry consists of the X axis, Y axis, line $𝑦 = m𝑥$, line $𝑦 = −m𝑥$, line $𝑥 = 𝑎$, line $𝑦 = 𝑏$ and towards the center point, namely point O (0,0).
- Rotation is a transformation that moves each point by the angle and center of rotation. If the rotation is clockwise then the angle is large negative. If the rotation is counterclockwise then the angle is positive. Center rotation consists of an origin point, namely O(0,0) and a certain point, namely P(a,b).
- Dilation is a transformation of the size or scale of a geometric figure (reduction/enlargement) but does not change the shape of the shape. Dilation is determined by the center and scale factors.
Come on, let’s discuss translation first!
Understanding Translation in Geometric Transformations
Translation has the meaning of shift or movement. Translation in geometric transformation is movement by shifting an object (usually in the form of points, curves, flat figures, etc.) according to a certain distance and direction. For example, we want to move a point from position A to position A B, there is a shift as far as $ a $ units in the horizontal direction and as far as $ b $ units in the vertical direction. So the transformation for type translation we can write in matrix form: $ T = \left( \begin{matrix} a \\ b \end{matrix} \right) $ .
To make it easier to understand the concept of translation, we can use the Cartesian plane approach. We can assume a shift to the right in the Cartesian plane it is the positive X axis, a shift to the left is the negative is the negative Y axis.
Pay attention to the following illustration!
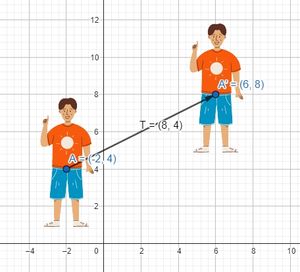
Suppose Trawan wants to go somewhere from the starting point A(-2,4). Trawan walked 8 units to the east and walk 4 units north. Can you determine the end point of Trawan?
If we look at the Cartesian plane, the coordinates of Trawan’s starting point are (-2.4). Next, Trawan walked east 8 units, meaning Trawan’s position shifted 8 units to the right from the initial position in the Cartesian plane. Next is Trawan walking again towards the north for 4 units, meaning Trawan’s position shifted 4 units upwards. If we look at the Cartesian plane at the end point Trawan’s position is at coordinates (6, 8). This is meaningful $$ \begin{pmatrix} -2 \\ 4 \end{pmatrix} + \begin{pmatrix} 8 \\ 4 \end{pmatrix} = \begin{pmatrix} 6 \\ 8 \end{pmatrix} $$
So, Trawan’s final position is located at coordinates (−4, −3)
To make it easier, here’s how to determine the shadow of the translation process in Geometric Transformation.
Translation Calculation Formula (How to Determine the Shadow of the Translation Transformation)
Translation (shift) is a transformation that moves points on field with a certain direction and distance.
Suppose any point $A(x,y) $ is translated by a translation matrix $ T = \begin{pmatrix} a \\ b \end{pmatrix} $, then we get the image, namely $ A^\prime (x^\prime , y^\prime ) $, we can tuliskan : $$ A(x,y) \xrightarrow[]{T = \begin{pmatrix} a \\ b \end{pmatrix}} A^\prime (x^\prime, y^\prime ) $$
How to calculate: $$ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} a \\ b \end{pmatrix} $$
So if we operate it becomes: $$ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} = \begin{pmatrix} x + a \\ y + b \end{pmatrix} $$
$ T = \begin{pmatrix}𝑎\\𝑏 \end{pmatrix} $ is called the translation component, 𝑎 is the horizontal shift and 𝑏 is the vertical shift.
Point 𝐴′ is called the transformed image of point 𝐴.
Examples of translation questions
Example 1
Determine the image of point A(3,-4) if translated by the matrix $ T=\left( \begin{matrix} -1 \\ 2 \end{matrix} \right) $
Solution ✍️
Determining the image of the point $A(3,-4)$ : $$ \begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} a \\ b \end{pmatrix} \\ &= \begin{pmatrix} 3 \\ -4 \end{pmatrix}+ \begin{pmatrix} -1 \\ 2 \end{pmatrix} \\ &= \begin{pmatrix} 3 +(-1)\\ -4+2 \end{pmatrix} \\ &= \begin{pmatrix} 4\\ -2 \end{pmatrix} \end{align*} $$ So, the image of point A is $ A^\prime (4,-2) $ 😄
Example 2
Determine the image of the parabolic curve $ 3x+2y=8 $ if translated by $T = \begin{pmatrix} -4 \ 1 \end{pmatrix} $!
Solution ✍️
- Because the equation or function is transformed, what we transform is the point $(x,y)$, after that we change it into the form $x^\prime $ and $ y^\prime $.
- The translation process: $$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} a \\ b \end{pmatrix} \\ \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix}+ \begin{pmatrix} -4 \\ 1 \end{pmatrix} \end{align*} $$
- change to $x=..$ and $y=…$ (move based on matrix similarity) $$\begin{align*} \begin{pmatrix} x^\prime \\ y^\prime \end{pmatrix} - \begin{pmatrix} -4 \\ 1 \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x^\prime + 4 \\ y^\prime -1 \end{pmatrix} &= \begin{pmatrix} x \\ y \end{pmatrix} \end{align*} $$ We get: $ x = x^\prime + 4 , $ and $ y = y^\prime - 1 $. We will substitute this form into the initial equation $3x+2y=8$ so that we get the image equation.
- Substitute the form $ x = x^\prime + 4 , $ and $ y = y^\prime - 1 $ into the initial equation $$ \begin{align*} 3x+2y&=8 \\ 3(x^\prime+4)+2(y^\prime-1)&=8 \\ 3x^\prime+12+2y^\prime-2&=8 \\ 3x^\prime+2y^\prime+10&=8 \\ 3x^\prime+2y^\prime&=-2 \end{align*} $$ So we get the image equation, namely $ 3x^\prime+2y^\prime=-2$ So, the image equation is $ 3x+2y=-2 $ 😄
Practice Translation Questions
To deepen your knowledge, please do the following practice questions!
- Determine the image of the point $𝐴(3, 5)$ by the translation $𝑇 \begin{pmatrix}−2\\4\end{pmatrix}$!
- The line $𝑙 ∶ 2𝑥 − 3𝑦 + 12 = 0$ is translated by $𝑇 \begin{pmatrix}1\\-2\end{pmatrix}$. Determine the equation for the translation of line 𝑙 by T!
