Geometric Transformations: Rotation | Class XI High School Mathematics

Easily learn the concept of Rotation as part of geometric transformation and become a Class XI High School Mathematics champion!

Hi Sinmat Friends, Tired of rotation questions that make you dizzy?

Have you ever watched the rotation of a fan blade, a car wheel, or a clock hand? In mathematics, this rotation phenomenon is studied in the concept of Rotation, which is a type of geometric transformation.

But how do you calculate it in mathematics?

This time Mimin will share complete material regarding rotation that you learned in class XI SMA or SMK. In this material you will learn the Basic Concept of Rotation and Types of Rotation.

Before starting, make sure you are familiar with:

• Geometric Transformations: Introduction to basic concepts.
• Cartesian Coordinate System: Reference point for calculations.
• Matrix Calculation Operations: Tools to solve rotation problems.

Come on, scroll down and start learning rotation like a master!

Understanding Rotation

Rotation is a geometric transformation that moves each point on a plane to another point by turning at a certain point.

Rotation on a plane is determined by:

1. Center point of rotation
2. Large rotation angle
3. Direction of rotation angle

Rotation Elements:

• Rotation Center Point: The point that is the reference point for rotational movement from the start point to the end point.
• Rotation Angle: The rotation angle measured in degrees. A positive rotation angle ($\alpha$) indicates a counterclockwise rotation direction, while a negative rotation angle ($-\alpha$) indicates a clockwise rotation direction.
• Orientation Angle: The angle formed by the line connecting the center of rotation with the start point and the line connecting the center of rotation with the end point.

Rotation is denoted by $R(P,\alpha)$ where $P$ is the center of rotation and $\alpha$ is the angle rotation

Types of Rotation (Turnover)

1. Determine the rotation of the point about the center (0, 0)

To understand the form of rotation at the center point (0, 0), we can observe the displacement of point A in the following image

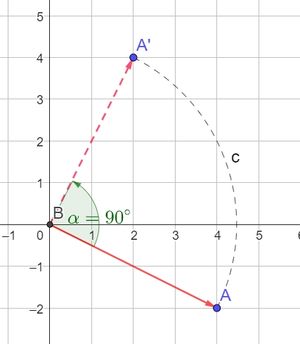
Suppose there is a point $𝐴(𝑥, 𝑦)$ which will be rotated by $\alpha$ with center (0, 0) and will produce a point $𝐴'(𝑥', 𝑦')$ and can be written as follows.

$$ A(x,y) \xrightarrow[]{R_{[O(0,0),\alpha]}} A' (x, -y ) $$

The point $(𝑥, 𝑦)$ is rotated by $\alpha$ about the center point $(0, 0)$ to produce a dot image $𝐴'(𝑥', 𝑦')$ with Steps:

1. Suppose the starting point is $A(x, y)$ and the rotation angle is $\alpha$.
2. Use the following rotation matrix:

$$\begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix}$$

3. Multiply the rotation matrix by the coordinates of the starting point:

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} $$

4. The coordinates of the end point $A'(x', y')$ are the result of the product.

Sample Question 1

Given that Point $A(4, -2)$ is rotated $90^\circ$ counterclockwise about the center $(0, 0)$. Determine the coordinates of point $A$ after rotation!

Solution ✍️

Point coordinates $A(4, -2)$ rotated $R_{(O,90^\circ)}$

Coordinates of point $P$ after rotation:

$$\begin{align*}\begin{bmatrix} x' \\ y' \end{bmatrix} &= \begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \\ &= \begin{bmatrix} \cos 90\degree & -\sin 90\degree \\ \sin 90\degree & \cos 90\degree \end{bmatrix} \begin{bmatrix} 4 \\ -2 \end{bmatrix} \\ &=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 4 \\ -2 \end{bmatrix} \\ &=\begin{bmatrix} 2 \\ 4 \end{bmatrix} \end{align*}$$

So, point $A$ after rotation becomes $A'(2,4)$.

2. Determine the Rotation of the Curve about the Center (0, 0)

Sample Question 2

It is known that the line $2𝑥 − 3𝑦 + 6 = 0$ is rotated by $180\degree$ about the center point (0, 0). Determine the equation of the line resulting from the rotation!

Solution ✍️

• find an equation that satisfies one of the points

  Suppose Point $A(x, y)$ through $2𝑥 − 3𝑦 + 6 = 0$ is rotated $R_{(O,180^\circ)}$ so that $$\begin{align*} \begin{bmatrix} x' \\ y' \end{bmatrix} &= \begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \\ &= \begin{bmatrix} \cos 180\degree & -\sin 180\degree \\ \sin 180\degree & \cos 180\degree \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \\ &=\begin{bmatrix} -1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} x4 \\ y \end{bmatrix} \\ \begin{bmatrix} x' \\ y' \end{bmatrix} &=\begin{bmatrix} -x \\ -y \end{bmatrix} \end{align*}$$

• Based on the similarity of the two matrices obtained $$\begin{align*} x'=-x \rightarrow x=-x' \\ y'=-y \rightarrow y=-y' \end{align*}$$

• Substitute $𝒙 = −𝒙'$ and $𝒚 = −𝒚'$ to the equation of the line $2𝑥 − 3𝑦 + 6 = 0$

  $$\begin{align*}2𝑥 − 3𝑦 + 6 = 0 \\ 2(-𝑥') − 3(-𝑦') + 6 = 0 \\ -2𝑥' + 3𝑦' + 6 = 0 \end{align*}$$

So, the equation of the rotation product line is −2𝑥 + 3𝑦 + 12 = 0

3. Determine the rotation of the point about the center (a, b)

To understand the form of rotation at the center point (a, b), we can observe the displacement of point A in the following image

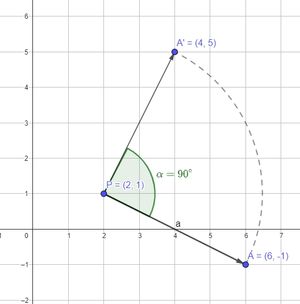
Suppose there is a point $𝐴(𝑥, 𝑦)$ which will be rotated $\alpha$ with center (a, b) and will produce a point $𝐴'(𝑥', 𝑦')$ and can be written as follows.

$$ A(x,y) \xrightarrow[]{R_{[(a,b),\alpha]}} A' (x, -y ) $$

The point $(𝑥, 𝑦)$ is rotated by $\alpha$ about the center point $(0, 0)$ to produce an image of the point $𝐴'(𝑥', 𝑦')$ with rule:

$$\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix} \begin{bmatrix} x-a \\ y-b \end{bmatrix} + \begin{bmatrix} a \\ b \end{bmatrix}$$

Sample Question 3

Given that Point $C(6, -1)$ is rotated $90^\circ$ counterclockwise about the center $(2, 1)$. Determine the coordinates of point $C$ after rotation!

Solution ✍️

Point coordinates $C(6, -1)$ rotated $R_{([2,1],90^\circ)}$

Coordinates of point $C$ after rotation:

$$\begin{align*}\begin{bmatrix} x' \\ y' \end{bmatrix} &= \begin{bmatrix} \cos\alpha & -\sin\alpha \\ \sin\alpha & \cos\alpha \end{bmatrix} \begin{bmatrix} x-a \\ y-b \end{bmatrix} + \begin{bmatrix} a \\ b \end{bmatrix} \\ &= \begin{bmatrix} \cos 90\degree & -\sin 90\degree \\ \sin 90\degree & \cos 90\degree \end{bmatrix} \begin{bmatrix} 6-2 \\ -1-1 \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} \\ &=\begin{bmatrix} 0 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} 4 \\ -2 \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} \\ &=\begin{bmatrix} 2 \\ 4 \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} \\ &=\begin{bmatrix} 4 \\ 5 \end{bmatrix} \end{align*}$$

So, point $C$ after rotation becomes $C'(4,5)$.

That’s what admin can give Remember!

• Don’t hesitate to ask if you need help.
• Practice directly to master the concept of rotation!