Translation or reflection in Geometric Transformations is class xi mathematics material, let's look at the definition, example questions, and how to determine the reflection below

Hi Sinmat Friends! Have you ever faced a mirror? Your image in the mirror is the result of a mathematical transformation called reflection. Exciting, right? After previously we studied Translation↝ , this time we will study geometric transformations, including reflection. Reflection is an important concept in geometry which describes how a geometric object can reflect or reflect itself on a certain line or plane.

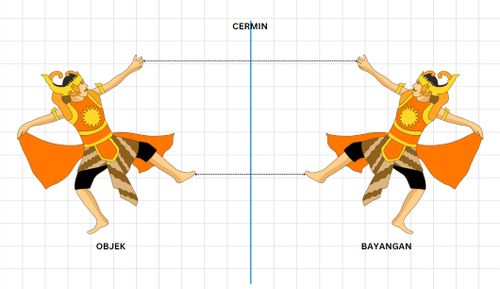
Pay attention to the following illustration Reflection Illustration

Gatotkaca stands in front of a mirror at a distance of 50 cm and Gatotkaca is 160 cm tall. What is the result of Gatotkaca’s reflection in the mirror? How far is Gatotkaca’s image from the mirror?

Friends, if we look in the mirror, the image of Gatotkaca is a figure of Gatotkaca with the same shape, height and distance of the image but the direction is facing each other, right? What do you think reflection is like, and what is its nature? let’s read in full.

Understanding Reflection in Geometric Transformations

Reflection (mirroring) is a transformation that moves each point on a plane using the properties of a mirror image. Reflection is symbolized by $𝑀_π‘Ž$ where $π‘Ž$ is the mirror axis.

Properties of Reflection

After looking at the illustration in the picture above, we can see the nature of reflection, namely

  1. The distance from the origin to the mirror is the same as the distance from the mirror to the image point
  2. The line connecting the origin point with the image point is perpendicular against the mirror
  3. Lines formed between the origin points and the points The shadows will be parallel to each other

Next, let’s discuss the types of reflection.

Types of Reflections in Geometric Transformations

1. Reflection of the $x$ axis

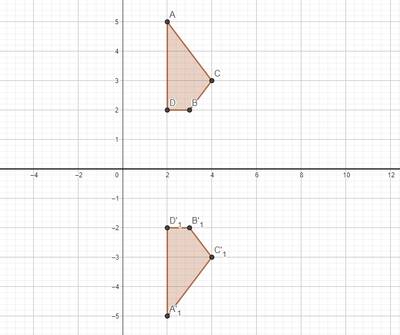Reflection on the x-axis For example, any point $A(x,y) $ reflected on the $x$ axis will produce an image $A'(x,-y)$. we can write it down

$$ A(x,y) \xrightarrow[]{M_{sbx}} A' (x, -y ) $$ or for example, the image $A'(x',y')$ can also be written in the form of a transformation matrix. The matrix is: $ M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $ as following $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} $$ **Example**

  1. If point $𝐡(-2, 5)$ is reflected about the $π‘₯$ axis, determine the image of point B!

    Solution ✍️

    $$ B(x,y) \xrightarrow[]{M_{sbx}} B' (x', y' ) $$ Calculate with matrix $$ \begin{align*}\begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} 1 & 0 \\ 0 &-1 \end{pmatrix} \begin{pmatrix} -2 \\ 5 \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \end{pmatrix} &= \begin{pmatrix} -2\\ -5 \end{pmatrix}\end{align*}$$

    So the image is $B'(-2,-5)$.

  2. If the line $𝑙: 3π‘₯ βˆ’ 2𝑦 βˆ’ 5 = 0$ is reflected on the $π‘₯$ axis then the resulting image of line $𝑙$ is… For example, the point $𝐴(π‘₯, 𝑦)$ satisfies the equation $3π‘₯ βˆ’ 2𝑦 βˆ’ 5 = 0$ so that the image of A is $A'(x',-y')$ (change the sign of y to the opposite) we obtain $$x = x' \\ y=-y' $$ Substitute $π‘₯ = π‘₯'$ and $𝑦 = βˆ’π‘¦'$ into the equation of line 𝑙 $$\begin{align*}3x-2y-5=0\\ 3x'-2(-y')-5=0\\ 3x'+2y'-5=0 \end{align*}$$ So, the image equation of line 𝑙 is $3π‘₯ + 2𝑦 βˆ’ 5 = 0$

2. Reflection of the $y$ axis

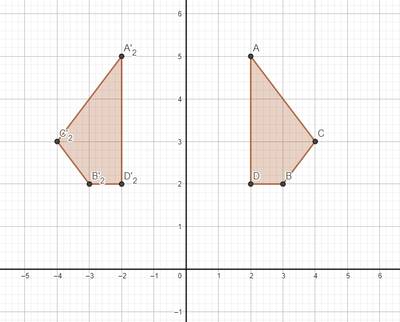Reflection on the x-axis For example, any point $A(x,y) $ reflected on the $y$ axis will produce an image $A'(-x,y)$. we can write it down

$$ A(x,y) \xrightarrow[]{M_{sby}} A' (x, -y ) $$ or for example, the image $A'(x',y')$ can also be written in the form of a transformation matrix. The matrix is: $ M = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} $ as following $$ \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} -1 & 0 \\ 0 &1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} $$ **Example**

  1. Determine the images of points A(1,2), B(3,-1) and C(-4,-6) when reflected on the Y axis!

    Solution ✍️

    • For this problem we do it all at once (not points A or B or C separately). how to use matrix multiplication $ M = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $
    • Image of points A(1,2), B(3,-1) and C(-4,-6) simultaneously: $$\begin{align*} \text{ bayangan } & = \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \times \text{ awal} \\ \begin{pmatrix}A' & B' & C' \end{pmatrix} & = \begin{pmatrix}1 & 0 \\ 0 & -1 \end{pmatrix} \times \begin{pmatrix}1 & 3 & -4 \\ 2 & -1 & -6 \end{pmatrix} \\ & = \begin{pmatrix}1 & 3 & -4 \\ -2 & 1 & 6 \end{pmatrix} \end{align*} $$ So, We get the respective shadows of $ A' (1,-2), B' (3,1) $ and $ C' (-4,6) $.

  2. If the line $𝑙: 2π‘₯ βˆ’ 3𝑦 + 12 = 0$ is reflected on the $Y$ axis then the resulting image of line $𝑙$ is…

    Solution ✍️

    • Reflection matrix on the Y axis: $ M = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} $
    • Determine the relationship $ (x,y) $ and $ (x' , y' ) $ : $$\begin{align*} \begin{pmatrix} x' \\ y' \end{pmatrix} & = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\\ \begin{pmatrix} x' \\ y' \end{pmatrix} & = \begin{pmatrix} -x \\ y \end{pmatrix} \end{align*} $$ We get: $$ x' = -x \rightarrow x = -x' \\ y' = y \rightarrow y = y' $$
    • Substitute the form $ x = -x' $ and $ y = y' $ into the initial equation so that we get the image equation: $$\begin{align*} 2π‘₯ βˆ’ 3𝑦 + 12 = 0 \\ 2(-π‘₯') βˆ’ 3𝑦' + 12 = 0 \\ -2x'-3y'+12=0 \text{ (kali -1) }\\ 2x'+3y'-12=0 \end{align*} $$ until the shadow $ 2x'+3y'-12=0 $ or $ 2x+3y-12=0 $.

    So, the image equation is $ 2x+3y-12=0$. πŸ˜„

3. Reflection of the origin $O(0,0)$

4. Reflection of the line $x=a$

5. Reflection of the line $y=b$

6. Reflection of the origin $P(a,b)$

7. Reflection of $y=x$

8. Reflection of the line $y=-x$

9. Reflection of the line $y=mx+c$

where $m=\tan \theta$