Geometric Interpretation of the Position of Two or More Vectors

Geometric Interpretation of the position of two or more vectors, Comparison of Two Vectors and Collinearity

1. Inline (collinear) vectors

Points P, N, and Q are said to be collinear if the vector constructed by two points between them can be expressed as the vector product of the other two points. Thus, if the points P, N and Q lie on a straight line, N is said to divide the line segment PQ in the ratio k, if $\overrightarrow{PN}~=k\text{ }\overrightarrow{NQ}$.

Definition of inline (collinear) points

Three points P, N, and Q are said to be collinear if and only if $(\Leftrightarrow )$

Example of Collinear Proof

The position vectors of P, Q, and R with respect to O are $\overline{p}=3\overline{b}+5\overline{c}-2\overline{a}$, $\overline{q}=\overline{ a}+2\overline{b}+3\overline{c}$, and $\overline{r}=7\overline{a}-c$. Show that the three points are aligned
Alternative solutions $$\begin{align*} \overrightarrow{OP}&=3\overline{b}+5\overline{c}-2\overline{a} \\\overrightarrow{OQ}&=\overline{a}+2\overline{b}+3\overline{c} \\\overrightarrow{OR}&=7\overline{a}-\overline{c} \end{align*}$$ $$\begin{align*} \overrightarrow{PQ}&=\overrightarrow{OQ}-\overrightarrow{OP} \\ \overrightarrow{PQ}&=(\overline{a}+2\overline{b}+3\overline{c})-(3\overline{b}+5\overline{c}-2\overline{a}) \\ \overrightarrow{PQ}&=3\overline{a}-\overline{b}-2\overline{c} \end{align*}$$ $$\begin{align*} \overrightarrow{PR}&=\overrightarrow{OR}-\overrightarrow{OP} \\ \overrightarrow{PR}&=(7\overline{a}-\overline{c})-(3\overline{b}+5\overline{c}-2\overline{a}) \\ \overrightarrow{PR}&=3(3\overline{a}-\overline{b}-2\overline{c}) \end{align*}$$ It can be seen that $\overrightarrow{PR}=3\overrightarrow{PQ}$ so that there is a number $k=3$ that makes the three points line up. (Proven)

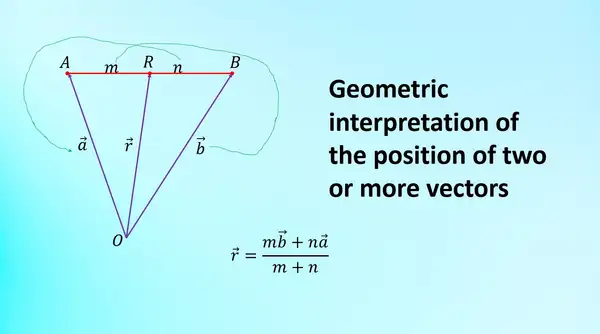
2. Comparison Formula

On the picture $PN:NQ=m:n$
maka $\overrightarrow{PN}=\frac{m}{n}\overrightarrow{NQ}$
until $k=\frac{m}{n}$ From this comparison, point N can be expressed as a position vector n in the position vector of points P and Q. The method is as follows $$\begin{align*} \overline{n}&=\overline{p}+\overrightarrow{PN} \\ \overline{n}&=\overline{p}+\frac{m}{m+n}\overrightarrow{PQ} \\ \overline{n}&=\overline{p}+\frac{m}{m+n}(\overline{q}-\overline{p}) \\ \overline{n}&=\frac{m\overline{p}+n\overline{p}+m\overline{q}-m\overline{p}}{m+n} \\ \overline{n}&=\frac{m\overline{q}+n\overline{p}}{m+n}\\ \therefore \overline{n}=\frac{m\overline{q}+n\overline{p}}{m+n} \end{align*}$$ If T is the midpoint of PQ and $m=n$ then the position vector $\overline{t}$ is determined by: $$\overline{t}=\frac{1}{2}(\overline{a}+\overline{b})$$

Example

Given ∆ABC with the position vectors of A, B, and C with respect to point O, namely $\overline{a}=3 \overline{p} +2\overline{q},$ $\overline{b}=-5 \overline{p}-3\overline{q},$and $\overline{c}=4\overline{p}-\overline{q}$. M is the midpoint of AB and point N is on AC such that $\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}.$ Determine the position vectors of M and N in the form $\overline{p}$ and $ \overline{q}$.

Alternative solutions
M is the midpoint of AB, meaning: $$\begin{align*} \overline{m}&=\overrightarrow{OM} \\ \overline{m}&=\frac{\overline{a}+\overline{b}}{2} \\ \overline{m}&=\frac{3\overline{p}+2\overline{q}-5\overline{p}-3\overline{q}}{2} \\ \overline{m}&=\frac{-2\overline{p}-\overline{q}}{2} \\ \therefore \overline{m}&=\overline{p}-\frac{1}{2}\overline{q} \end{align*}$$

$\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}$ means N divides AC in the ratio 1:2

$\therefore \overrightarrow{ON}=\frac{2\overrightarrow{OA}+1\overrightarrow{OC}}{1+2}$ $$\begin{align*} \overline{n}&=\frac{2(3\overline{p}+2\overline{q})+4\overline{p}-\overline{q}}{3} \\ \overline{n}&=\frac{10\overline{p}+3\overline{q}}{3} \\ \overline{n}&=\frac{10}{3}\overline{p}+\overline{q} \end{align*}$$

3. Understanding linear combinations and bases

If $ \overline{v_1},\overline{v_2},\overline{v_3},…,\overline{v_n}$ are Vectors in the space $R^2$. Then for each Vector $\overline{v}\in R^2$, the Vector $\overline{v}$ can be expressed as a linear combination in $\overline{v_1},\overline{v_2},\overline{v_3}, …,\overline{v_n}$ namely:

$\vec{v}=k_1\vec{v}_1+k_2\vec{v}_2+k_3\vec{v}_3+…+k_n\vec{v}_n$ dengan $k_1,k_2,k_3, …,k_n$ adalah scalar-scalar real. If $k_1,k_2,k_3,…,k_n$ tunggal, maka Vector-vector $\vec{v}_1,\vec{v}_2,\vec{v}_3,…,\vec{v }_n$ is called basis dalam ruang $R^2$

Look at the following image, showing two non-parallel and unidirectional vectors $\overline{u}$ and $\overline{v}.$ If $\overrightarrow{OC}=q.\overline{v}$ and $\overrightarrow{OB}=p.\overline{u}$ with $p$ and $q$ constant, based on the parallelogram rule we obtain: $\overrightarrow{OA}=\overline{a}=p.\overline{u}+q.\overline{v}$ This means that the vector $\overline{a}$ is formed from the linear combination $p.\overline{u}$ and $q.\overline{v}$ with $\overline{u}$ and $\overline{v}$ basis for Vector $\overline{a}.$

Example

From $∆OAB$ it is known that C is in AB and D is in OB. T at the intersection of OC and AD. Comparison AC:CB = 2:1 and OD:DB = 1:3. Define OT:TC !

Alternative solutions
Because OAB and its components lie in a plane, it has dimensions of 2 (two). For this reason, every 2 vectors that are not in the same direction will be a basis for R. As a result, each vector can be expressed as a linear combination of the two bases singly.
Suppose the bases are OA and OB (vectors OA = a and OB = b), then $$\begin{align*} \overrightarrow{AC}&=\frac{2}{3}\overrightarrow{AB} \\ \overrightarrow{AC}&=\frac{2}{3}(\overrightarrow{AO}+\overrightarrow{OB}) \\ \overrightarrow{AC}&=\frac{2}{3}(-\overline{a}+\overline{b})………(1) \end{align*}$$

$$\begin{align*} \overrightarrow{AD}&=\overrightarrow{AO}+\overrightarrow{OD} \\ \overrightarrow{AD}&=\overrightarrow{AO}+\frac{1}{4}\overrightarrow{OB}) \\ \overrightarrow{AC}&=-\overline{a}+\frac{1}{4}\overline{b}……….(2) \end{align*}$$

Karena $\overrightarrow{OT}$ searah dengan $\overrightarrow{OC}$ maka $\overrightarrow{OT}=\lambda \overrightarrow{OC}$ , $\lambda $ suatu Scalar $$\begin{align*} \overrightarrow{OT}&=\lambda \overrightarrow{OC} \\ \overrightarrow{OT}&=\lambda (\overrightarrow{OA}+\overrightarrow{AC}) \\ \overrightarrow{OT}&=\lambda (\overline{a}+\frac{2}{3}(-\overline{a}+\overline{b}) \\ \overrightarrow{OT}&=\frac{1}{3}\lambda \overline{a}+\frac{2}{3}\lambda \overline{b}………..(3) \end{align*}$$ On the other hand $\overrightarrow{AT}$ is in the same direction as $\overrightarrow{AD}$ so $\overrightarrow{AT}=\mu \overrightarrow{AD}$ , $\lambda $ is a Scalar $$\begin{align*} \overrightarrow{OT}&=\overrightarrow{OA}+\overrightarrow{AT} \\ \overrightarrow{OT}&=\overline{a}+\mu (-\overline{a}+\frac{1}{4}\overline{b}) \\ \overrightarrow{OT}&=(1-\mu )\overline{a}+\frac{1}{4}\mu \overline{b}…………..(4) \end{align*}$$ By equating the coefficients $\overline{a}$ and $\overline{b}$ in (3) and (4), namely:
The coefficient $\overline{a}$ obtains $1-\mu =\frac{1}{3}\lambda $
The coefficient $\overline{b}$ is obtained $\frac{1}{4}\mu =\frac{2}{3}\lambda $ then $\mu =\frac{8}{3}\lambda $
$\mu =\frac{8}{3}\lambda $ substituted into $1-\mu =\frac{1}{3}\lambda $ is obtained $$\begin{align*} 1-\frac{8}{3}\lambda &=\frac{1}{3}\lambda \\ 1&=\frac{9}{3}\lambda \\ \lambda &=\frac{1}{3} \end{align*}$$ $\lambda =\frac{1}{3}$ substituted into $\mu =\frac{8}{3}\lambda $ is obtained $$\begin{align*} \mu &=\frac{8}{3}.\frac{1}{3} \\ \mu &=\frac{8}{9} \end{align*}$$ Karena $\overrightarrow{OT}=\lambda \overrightarrow{OC}$dan $\lambda =\frac{1}{3}$ maka $\overrightarrow{OT}=\frac{1}{3}\overrightarrow{OC}$

Selanjutnya karena $\overrightarrow{OT}=\frac{1}{3}\overrightarrow{OC}$ maka $\left| \overrightarrow{OT} \right|=\frac{1}{3}\left| \overrightarrow{OC} \right|$atau $\frac{OT}{OC}=\frac{1}{3}$
Terakhir karena $\frac{OT}{OC}=\frac{1}{3}$ maka $\frac{OT}{TC}=\frac{1}{(3+1)}=\frac{1} {2}$ or $OT:TC=1:2$
So, the OT:TC ratio is 1:2

Exercise 2

1. Known ABC Point D on BC such that BD:DC = 2:1. Point E is in the middle of AB If Z is the point of intersection of AD and CE, determine AZ:ZD = … and CZ:ZE = ….

2. Given the rectangle ABCD, points M and N are located in the middle of AB and DC respectively. Points P and Q are respectively the intersection points of the diagonal AC with the line segments DM and BN. Prove that AP = PQ = QC = $\frac{1}{3}$AC.

3. Theorems of Menelaus
   Given ∆ABC with a transversal (a line that intersects the sides of a triangle or its extension) PR. Prove that $\frac{AR}{RB}\times \frac{BQ}{QC}\times \frac{CP}{PA}=1$

4. Evidence of Something
   Triangle ∆ABC with AQ, BR, and CP intersects at point Z. Points P, Q, and R lie on line segments AB, BC, and CA, respectively. Prove that $\frac{AP}{PB}\times \frac{BQ}{QC}\times \frac{CR}{RA}=1$