Learn dilation in geometric transformations! Master the formulas and example problems. This material is specifically designed for Class XI high school students and mathematics teachers.
Hi Sinmat Friends, Have you ever been amazed by detailed close-up photos of insects? Confused about reading a large city map? Dilation, the “unexpected hero” of mathematics, plays an important role behind it!
For those of you Class XI high school students who are studying Geometry Transformations, this material is a must to master! Dilation is not only impressive but also widely applied in various fields, you know.
What is dilation?
Dilation is a transformation that can enlarge or reduce a flat shape proportionally, like a camera lens that magnifies an object without changing its shape.
Dilation is not just a mathematical concept, but a bridge to the amazing world of transformation! Master the concept and deepen your insight in seeing a world that can be enlarged or reduced.
Before starting, make sure you are familiar with:
- Geometric Transformations: Introduction to basic concepts.
- Cartesian Coordinate System: Reference point for calculations.
- Matrix Calculation Operations: Tools to solve rotation problems.
Come on, if you are familiar, let’s start…
1. Definition of Dilation
Dilation is a geometric transformation that enlarges or reduces a geometric figure without changing its shape. The reference point used to enlarge or reduce geometric figures is called dilation center. The factor that determines the enlargement or reduction of a geometric figure is called the scale factor.
Properties of dilation:
- A straight line that is dilated will produce a straight line.
- The dilated angle does not change in magnitude.
- The area of the dilated plane shape will change with the scale factor squared.
- The volume of the dilated shape will change by a scale factor cubed.
Figures that are enlarged or reduced (dilated) with scale 𝑘 can change size or stays the size but does not change the shape.
- If 𝑘 > 1 then the shape will be enlarged and located in the direction of the corner dilatation with reawakening
- If 𝑘 = 1 then the shape does not change in size or location
- If 0 < 𝑘 < 1 then the shape will be reduced and located in the direction of center of dilatation with reawakening.
- If −1 < 𝑘 < 0 then the shape will be reduced and lie in the opposite direction against the center of dilatation by waking up again
- If 𝑘 = −1 then the shape will not change shape and size and located in the opposite direction to the center of dilatation with the wake.
- If 𝑘 < −1 then the shape will be enlarged and located in the opposite direction against the center of dilatation by waking up again.
2. Determine Point Dilation at Center (0, 0)
Look at the following image
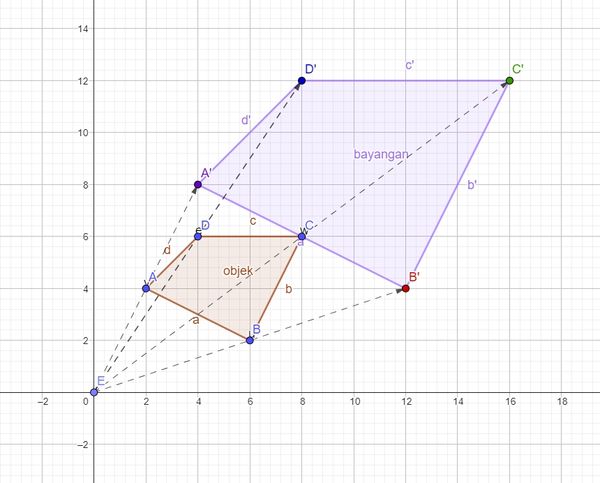
If a point $P(x, y)$ is dilated with a dilation center $(0, 0)$ and a scale factor $k$, then its image $P'(x', y')$ is calculated by the following formula:
$$x' = kx \quad \text{dan} \quad y' = ky$$
Example:
The point $P(2, 3)$ is dilated with a dilation center $(0, 0)$ and a scale factor of 3. The image of the point $P$ is $P'(x', y')$. Calculate the coordinates of $P'$.
Solution:
Based on the dilation formula, then:
$$x' = 3 \cdot 2 = 6$$
$$y' = 3 \cdot 3 = 9$$
So, the image coordinates of point $P'$ are $(6, 9)$.
3. Determine Curve Dilation at Center (0, 0)
If a curve $y = f(x)$ is dilated with a dilation center $(0, 0)$ and a scale factor $k$, then the image of the curve $y' = f'(x)$ is calculated using the following formula:
$$y' = k \cdot f(x)$$
Example:
The curve $y = x^2$ is dilated with a dilation center $(0, 0)$ and a scale factor of 2. The image of the curve $y'$ is $y' = f'(x)$. Calculate the equation $y'$.
Solution:
Based on the curve dilation formula, then:
$$y' = 2 \cdot x^2$$
So, the curve image equation is $y' = 2x^2$.
4. Determine the Dilation of Points at the Center (𝑎, 𝑏)
Look at the following image
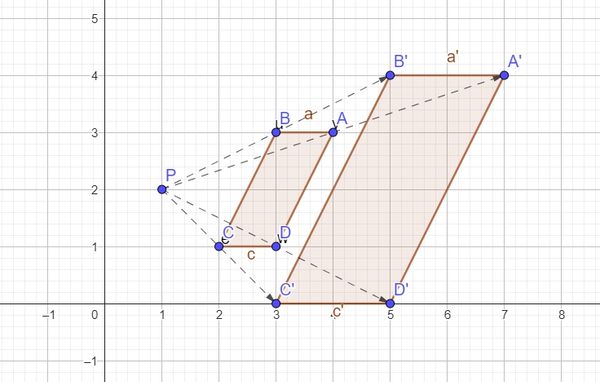
If a point $P(x, y)$ is dilated with a dilation center $(𝑎, 𝑏)$ and a scale factor $k$, then its image $P'(x', y')$ is calculated using the following formula:
$$x' = k(x - a) + a \quad \text{dan} \quad y' = k(y - b) + b$$
Example:
The point $P(2, 3)$ is dilated with a dilation center $(1, 2)$ and a scale factor of 2. The image of the point $P$ is $P'(x', y')$. Calculate the coordinates of $P'$.
Solution:
Based on the dilation formula, then:
$$x' = 2(2 - 1) + 1 = 3$$
$$y' = 2(3 - 2) + 2 = 4$$
So, the image coordinates of point $P'$ are $(3, 4)$.
5. Determine the Dilation of the Curve at the Center (𝑎, 𝑏)
If a curve $y = f(x)$ is dilated with a dilation center $(𝑎, 𝑏)$ and a scale factor $k$, then the image of the curve $y' = f'(x)$ is calculated using the following formula:
$$y' = k \cdot [f(x - a) + b]$$
Example:
The curve $y = x^2$ is dilated with a dilation center $(1, 2)$ and a scale factor of 2. The image of the curve $y'$ is $y' = f'(x)$. Calculate the equation $y'$.
Solution:
Based on the curve dilation formula, then:
$$y' = 2 \cdot [x^2 - (1) + 2]$$
$$y' = 2x^2 + 2$$
So, the curve image equation is $y' = 2x^2 + 2$.
That’s what admin can give Remember!
- Don’t hesitate to ask if you need help.
- Hands-on practice to master the concept of Dilation!
