change Cartesian coordinates to polar coordinates and vice versa in trigonometry
This time we will discuss how to convert or convert Cartesian coordinates to polar coordinates or vice versa, namely from polar coordinates to Cartesian coordinates. The coordinates of a point can be expressed in the form of polar coordinates and Cartesian coordinates. Polar coordinates are very useful in navigation science. Polar coordinates are also often called polar coordinates. Before continuing, study angle relations in trigonometry and also trigonometry values in various quadrants…
Understanding Cartesian Coordinates
Briefly, Cartesian coordinates are a point drawn on the x-axis and y-axis, consisting of the abscissa (x value) and ordinate (y value), written . The term Cartesian itself was discovered by a French mathematician named Rene Descartes. The result of this discovery was a combination of algebra and geometry which later developed into the sciences of analytical geometry, calculus and cartography.
The Cartesian coordinate system can also be used in higher dimensions, for example 3 dimensions using the x, y and z axes. If the x and y axes are used in 2 dimensions, then the z axis is perpendicular to the x and y axes.
The benefits of Cartesian coordinates are widely used in everyday life. Usually Cartesian coordinates are used in floor plans or maps, so that it makes it easier to find an area. Apart from that, Cartesian coordinates are also used in aviation so that planes do not collide with other planes.
Understanding polar coordinates (poles)
Polar coordinates or polar coordinates are a 2-dimensional coordinate system, where plane points are determined from predetermined point distances and angle sizes are determined from predetermined directions.
From the 8th century AD, the use of polar coordinates was developed to calculate the direction and distance of the Qibla from all corners of the earth.
Polar coordinates are coordinates drawn on the x and y axes, consisting of the value r () and the angle θ, which is the angle formed by lines OP and OX , written . Note the following relationship between polar coordinates and Cartesian coordinates.
Relationship between Cartesian Coordinates and Polar Coordinates
The relationship between Cartesian coordinates and polar coordinates is shown in the following figure.
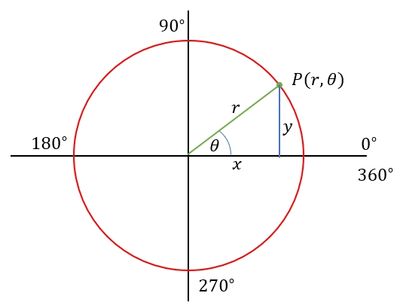
Conversion from Cartesian Coordinates to Polar Coordinates
From the picture above, we can get the relationship that if the Cartesian coordinates of the point are known then the polar coordinates can be determined in steps and using the following formula.
- Determine the value of
- Determine the angle or tan what is the value of y per x. Also pay attention to the location of the quadrants
Conversion from Polar Coordinates to Cartesian Coordinates
Look at the picture above again… If the polar coordinates of the point are known then the Cartesian coordinates of the point can be determined by using the following steps and formula.
- Determine the value of
- Determine the value of
Problems example
Express the following points in polar coordinates.
Solution ✍️
point meaning and
- Determine the radius ():
- Determine the angle with the formula:
Since the value is positive and is positive, then point P is in quadrant I with an angle So, the polar coordinates are .
points meaning and
- Determine the radius ():
- Determine the angle with the formula: $ \tan \theta = \dfrac{y}{x} $ $$\begin{align*} \tan\theta &= \frac{y}{x}\\\tan\theta&= \frac{3\sqrt{3}}{-3}\\\ tan\theta&= -\sqrt{3} \text{ (heart sign -)}\\\theta&= \arctan \sqrt{3} \\ \theta&= 60^\circ \end{align* }$$
Because the value $ x $ is negative and $ y $ is positive, then point Q is in quadrant II so the angle $ 180^\circ - 60^\circ =120^\circ$ So, the polar coordinates are $ P (6, 120^\circ) $ .
Express the following points in Cartesian coordinates.
- $P(4,45^\circ)$
- $Q(10,120^\circ)$
Solution ✍️
point $P(4.45^\circ)$ meaning $ r = 4$ and $ \theta = 45^\circ $
- Determine the value of $x$: $$\begin{align*} x &= r\cos\theta \\&= 4\cdot\cos 45^\circ \\&= 4\cdot \frac{1}{2}\sqrt{2} \\&= 2\sqrt{2} \end{align*}$$
- Determines the value of $y$ $$\begin{align*} y &= r\sin\theta \\&= 4\cdot\sin 45^\circ \\&= 4\cdot \frac{1}{2}\sqrt{2} \\&= 2\sqrt{2} \end{align*}$$
So, the Cartesian coordinates are $ P (4\sqrt{2}, 4\sqrt{2}) $ .
2nd titic $Q(10.120^\circ)$ meaning $ r = 10$ and $ \theta = 120^\circ $ - Determine the value of $x$: $$\begin{align*} x &= r\cos\theta \\&= 10\cdot\cos 120^\circ\\&= 10\cdot\cos (180^\circ-60^\circ)\\&= 10\cdot(-\cos 60^\circ) \\&= 10\cdot (-\frac{1}{2}) \\&= -5 \end{align*}$$ - Determines the value of $y$ $$\begin{align*} y &= r\sin\theta \\&= 10\cdot\sin 120^\circ\\&= 10\cdot\sin (180^\circ-60^\circ)\\&= 10\cdot(\sin 60^\circ) \\&= 10\cdot (\frac{1}{2}\sqrt{3}) \\&= 5\sqrt{3} \end{align*}$$
So, the Cartesian coordinates are $ P (-5, 5\sqrt{3}) $ .
