This vector comparison is actually the same as the multiplication of a scalar with a vector which we studied in the article Geometric Interpretation of the Position of Two or More Vectors. This time we will study in more depth the coordinates of the dividing points.

Table Of Contents

In this article we will learn about Vector Comparison of Line Segments. This vector comparison is actually the same as scalar multiplication with vectors which we have studied in the article Geometric Interpretation of the Position of Two or More Vectors↝ . This time we will study in more depth the coordinates of the dividing points.

There are three things we will learn in the Vector Comparison material, namely being able to determine the division of a line segment using the ratio m:n, determining the division formula in vector form and determining the coordinates of the dividing points on line segments and vectors. Before studying this material, friends must first master previous vector material such as vector concepts↝ , vector operations↝ , geometric interpretation of vectors↝ .

1. Division of line segments in the ratio m:n

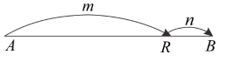
A point R divides the line segment $AB$ in the ratio $m:n$ if $AR:RB=m:n$. In the ratio $AR:RB=m:n$ there are two possible locations of point R on line segment AB, namely:

  1. Point R is located between points A and B (divides AB inside), divide AB in $$\begin{align*} & AR:RB=m:n \\&AR:AB=m:(m+n) \end{align*}$$

  2. Point R is located before or after points A and B (dividing AB outside). divide AB outside $$\begin{align*} & AR:RB=m:-n \\&AR:AB=m:(m-n) \end{align*}$$

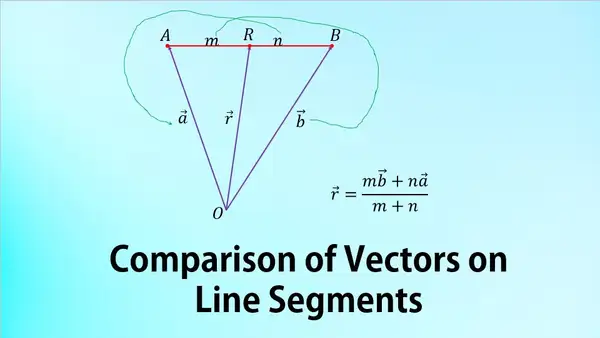
2. Division formula in Vector form

In the picture below, the ARB is in line (collinear). vector division $$\begin{align*} & AR:RB=m:n \\ &\Leftrightarrow \frac{AR}{RB}=\frac{m}{n}\\ &\Leftrightarrow nAR=mRB \end{align*}$$ For $$\begin{align*} & \text{}nAR=mRB \\ &\Leftrightarrow n(\vec{r}-\vec{a})=m(\vec{b}-\vec{r}) \\ &\Leftrightarrow \text{ }n\vec{r}-n\vec{a}=m\vec{b}-m\vec{r} \\ &\Leftrightarrow (m+n)\vec{r}= m\vec{b}+n\vec{a} \\ &\Leftrightarrow \text{ }\vec{r}=\frac{m\vec{b}+n\vec{a}}{m+ n} \end{align*}$$

3. Comparison formula in coordinate form

Previously we had formulated the division of line segments in vector form, namely: $$\vec{r}=\frac{m\vec{b}+n\vec{a}}{m+n}$$ For

  1. If $A(x_1,y_1)$ and $B(x_2,y_2)$ are in ${{R}^{2}}$, then $$\vec{r}=\frac{m\left( \begin{matrix}x_2 \\ y_2\\\end{matrix} \right)+n\left( \begin{matrix}x_1 \\ y_1\\\end{matrix} \right)}{ m+n}$$ Koordinat titik R adalah $R\left( \frac{mx_2+nx_1}{m+n},\text{ }\frac{my_2+ny_1}{m+n} \right)$
  2. If $A(x_1,y_1,{z_1})$ and $B(x_2,y_2,{z_2})$ in ${{R}^{2}}$, then $$\vec{r}=\frac{m\left( \begin{matrix}x_2\\y_2\\z_2\\\end{matrix} \right)+n\left( \begin{matrix}x_1\\y_1\\z_1\end{matrix} \right)}{m+n}$$ Koordinat titik R adalah $R\left( \frac{mx_2+nx_1}{m+n},\text{ }\frac{my_2+ny_1}{m+n},\text{ }\frac{mz_2+nz_1}{m+n} \right)$

Examples of Vector Comparison questions on Line Segments

Example 1

Determine the coordinates of the point P that divides the connecting line $A(2,3,-1) $ and $B(-3,3, 4) $ with the ratio $ 2 : 3 $ based on the determination:

  1. Point P divides AB inside,
  2. Point P divides AB outside and determine the position where point P is located.

Solution:

  1. Point P divides AB inside,
    • The comparison form is $\vec{AP} : \vec{PB} = 2 : 3 $
    • Determine the position vector of point P: $$\begin{align*} \vec{p} &= \frac{2\vec{b} + 3\vec{a}}{2+3} \\ &= \frac{1}{5 } (2\vec{b} + 3\vec{a}) \\ &= \frac{1}{5} (2(-3,3, 4) + 3(2,3,-1) ) \\ &= \frac{1}{5} ((-6,6, 8) + (6,9,-3)) \\ &= \frac{1}{5}(0 ,15, 5)\\ &=(0,3, 1) \end{align*}$$ We obtain the position vector of point P, namely $ \vec{p} =(0,3, 1)$ so that the coordinates point P is(0,3, 1).
  2. Point P divides AB outside and determine the position where point P is located.
    • The vector ratio $ m : n =2 : 3 $ means $ m : n $ so that point P lies before line AB.
    • The comparison form is $\vec{PA} : \vec{PB} = 2 : 3 $ or $\vec{AP} : \vec{PB} = -2 : 3 $
    • Determine the position vector of point P: $$\begin{align*} \vec{p} &= \frac{-2\vec{b} + 3\vec{a}}{-2+3} \\&= \frac{-2\vec{b} + 3\ vec{a}}{1} \\&= -2\vec{b} + 3\vec{a} \\&=-2(-3,3, 4) + 3(2,3 ,-1)\\&=(6,-6, -8) + (6,9,-3) \\&=(12,3, -11) \end{align*}$$ We obtain the position vector of point P, namely $ \vec{p} =(12,3, -11)$ so that the coordinates of point P are $ (12,3, -11) $ which is located before points A and B.

Example 2

Determine the coordinates of point C which divides the line $P(2,-3,3) $ and $Q(2,4,3)$ in the ratio $5 : 2$ based on the determination:

  1. Point C divides PQ inside,
  2. Point C divides PQ outside and determine the position where point C is located.

Solution:

  1. Point C divides PQ inside,
    • The comparison form is $\vec{PC} : \vec{CQ} = 5 : 2 $
    • Determine the position vector of point C: $$\begin{align*} \vec{c} &= \frac{5\vec{q} + 2\vec{p}}{5 + 2} \\ &= \frac{1}{7} (5\vec{q} + 2\vec{p}) \\&= \frac{1}{7} (5(2,4, 3) + 2(2,-3,3)) \\ &= \frac {1}{7} ((10,20, 15) + (4,-6,6)) \\ &= \frac{1}{7}(14,14, 21)\\& =(2 , 2, 3) \end{align*}$$ We obtain the position vector of point C, namely $ \vec{c} =(2 , 2, 3)$ so the coordinates of point C are (2 , 2, 3).
  2. Point C divides PQ outside and determine the position where point C is located.
    • The vector ratio is $ m : n =5 : 2 $ meaning $ m > n $ so that point C lies after line PQ.
    • The comparison form is $\vec{PC} : \vec{QC} = 5 : 2 $ or $\vec{PC} : \vec{CQ} = 5 : -2 $
    • Determine the position vector of point C: $$\begin{align*} \vec{c} &= \frac{5\vec{q} - 2\vec{p}}{5 - 2} \\ &= \frac{1}{3} (5\vec{q} - 2\vec{p}) \\ &= \frac{1}{3} (5(2,4, 3) - 2(2,-3,3)) \\ &= \frac{1}{3} ((10,20, 15) - (4,-6,6)) \\ &= \frac{1}{3}(6,26,9)\\ &=\left(2,\frac{26}{3}, 3 \right) \end{align*}$$ We obtain the position vector of point C, namely $ \vec{c} =\left(2,\frac{26}{3}, 3 \right)$ so that the coordinates of point C are $ \left(2,\frac{26}{3}, 3 \right)$ which is located after points P and Q.

Example 3

Determine the coordinates of the point P which lies outside AB with $ A(-3, 2 , 1 ) $ , $ B( 1, -2, 4) $ $ \vec{AP} : \vec{PB} = 3 : (-2) $ and determine the location of point P!

Solution:

  • In the comparison $ \vec{AP} : \vec{PB} = 3 : (-2) $, the twin point (point P) is already in the middle so we don’t need to reverse the direction of the vector. To do this directly, we use “near-near-far-far”.
  • Determine the position vector of point P: $$\begin{align*} \vec{p} &= \frac{3\vec{b} - 2\vec{a}}{3 - 2} \\ &= \frac{3\vec{b} - 2\vec{a }}{1} \\ &=3\vec{b} - 2\vec{a} \\ &=3( 1, -2, 4) - 2(-3, 2 , 1 ) \ \\ &=( 3, -6, 12) - (-6, 4 , 2 ) \\ &=( 9, -10, 10) \end{align*}$$ We obtain the position vector of point P, namely $ \vec{p} =( 9, -10, 10)$
    so that the coordinates of point P are $ (9, -10, 10) $.
  • Determine whether the location of point P is before or after AB: Pay attention to the vector ratio, namely $ 3 : -2 $, if we absolute it then we get the ratio to be $ 3 : 2 $, meaning $ m : n = 3 : 2 $ which satisfies $ m : n $ so that point P lies after the line segment AB.

Example 4

If $ \vec{a} $ , $ \vec{b} $ and $ \vec{c} $ are the position vectors of points A, B, and C of $ \Delta ABC $. Point D is on $ \vec{AC} $ so that $ AD : DC = 1 : 3 $ . Point E is on $ \vec{BC} $ so that $ BE : EC = 5 : 2 $. Express $ \vec{DE} $ in $ \vec{a} $ , $ \vec{b} $, and $ \vec{c} $ !

Solution:

  • Look at the following picture illustration:
    example solution 4
  • Determine the position vector D with the vector ratio $ AD : DC = 1 : 3 $ $$\begin{align*} \vec{d} &= \frac{1.\vec{c} + 3\vec{a} }{1 + 3}\\ &= \frac{\vec{c} + 3\vec{a } }{4} \end{align*}$$
  • Determine the position vector E with the vector ratio $ BE : EC = 5 : 2$ $$\begin{align*} \vec{e} &= \frac{5\vec{c} + 2\vec{b} }{5 + 2}\\ &= \frac{5\vec{c} + 2\vec{b } }{7} \end{align*}$$
  • Determining the vector $ \vec{DE} $ : $$\begin{align*} \vec{DE} &= \vec{e} - \vec{d}\\&= \frac{5\vec{c} + 2\vec{b} }{7} - \frac{\vec {c} + 3\vec{a} }{4} \\&= \frac{4(5\vec{c} + 2\vec{b}) }{28} - \frac{7(\ vec{c} + 3\vec{a} )}{28} \\&= \frac{20\vec{c} + 8\vec{b} }{28} - \frac{7\vec{ c} + 21\vec{a}}{28} \\&= \frac{20\vec{c} + 8\vec{b} - 7\vec{c} - 21\vec{a} } {28}\\&= \frac{- 21\vec{a} + 28\vec{b} - 7\vec{c} }{28}\\&= \frac{1}{28 } ( - 21\vec{a} + 28\vec{b} - 7\vec{c}) \end{align*}$$ Yes, the result is $ \vec{DE} = \frac{1}{28} (- 21\vec{a} + 28\vec{b} - 7\vec{c})$.

Example 5

From triangle ABC, it is known that points D are on AC and E are on AB. Point G at the intersection of DB and EC. If the comparison is known $ AD : DC = 3 : 1 $ and $ AE : EB = 1 : 2 $, then determine the ratio of $ EG : GC $ and $ DG : GB $!

Solution:

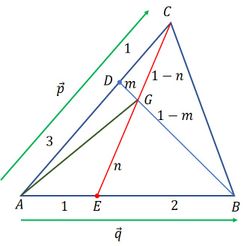
  • Look at the following picture illustration example solution 4 In the picture we series the line segment AG. To determine the required line ratio, we will work using the concept of vector comparison.
  • With the concept of collinear points, we get:
    Let $ \vec{AB} = \vec{q} $ and $ \vec{AC} = \vec{p} $.
    $ \vec{AE} = \frac{1}{3}\vec{AB} = \frac{1}{3}\vec{q} $ given $ \vec{AD} = \frac{3}{4 }\vec{AC} = \frac{3}{4}\vec{p} $.
    • The vector $\vec{EG} $ is in line with $ \vec{EC} $ until multiplication occurs:
      $ \vec{EG} = n\vec{EC} \rightarrow \frac{\vec{EG}}{\vec{EC}} = \frac{n}{1} $sehingga $ \frac{\vec{EG }}{\vec{GC}} = \frac{n}{1-n} $
    • The vector $\vec{DG} $ is in line with $ \vec{DB} $ until multiplication occurs:
      $ \vec{DG} = m\vec{DB} \rightarrow \frac{\vec{DG}}{\vec{DB}} = \frac{m}{1} $sehinga $ \frac{\vec{GG }}{\vec{GB}} = \frac{m}{1-m} $
  • Menentukan vector $ \vec{AG} $ dari $ \vec{EG}:\vec{GC} = n : 1-n $ $ \vec{AG} = \frac{n\vec{AC} + (1-n)\vec{AE}}{n + (1-n)} = \frac{n\vec{p} + (1 -n).\frac{1}{3}\vec{q}}{1} = n\vec{p} + \frac{1-n}{3}\vec{q} $.
  • Menentukan vector $ \vec{AG} $ dari $ \vec{DG}:\vec{GB} = m : 1-m $ $ \vec{AG} = \frac{m\vec{AB} + (1-m)\vec{AD}}{m + (1-m)} = \frac{m\vec{q} + (1 -m).\frac{3}{4}\vec{p}}{1} = m\vec{q} + \frac{3(1-m)}{4}\vec{p} $.
  • The vector $ \vec{AG} $ of the two forms above is the same so that by equating the coefficients of similar vectors, we get the equation:
    • Vector coefficients $ \vec{p} $ : $$ n = \frac{3(1-m)}{4} \rightarrow 4n = 3 - 3m \rightarrow 4n + 3m = 3….(1)$$
    • Vector coefficients $ \vec{q} $ : $$ \frac{1-n}{3} = m \rightarrow 1 - n = 3m \rightarrow n + 3m = 1….(2)$$
    • Elimination of press(1) and press(2): $$ \begin{array}{cc}4n + 3m = 3 &\\ n + 3m = 1 & -\\\hline 3n = 2 &\\ n = \frac{2}{3 } \end{array} $$ Pers(2): $ n + 3m = 1 \rightarrow \frac{2}{3} + 3m = 1 \rightarrow m = \frac{1}{9} $.
  • Determine the requested comparison:
    • Perbandingan $\vec{EG}:\vec{GC} $ $$\vec{EG}:\vec{GC} = n : 1-n = \frac{2}{3} : 1 - \frac{2}{3} = \frac{2}{3} : \frac{1}{3} = 2 : 1 $$
    • Perbandingan $ \vec{DG}:\vec{GB}$ : $$ \vec{DG}:\vec{GB} = m : 1-m= \frac{1}{9} : 1 - \frac{1}{9} = \frac{1}{9} : \ frac{8}{9} = 1 : 8 $$

So, we get the ratio $ EG : GC = 2 : 1 $ and $ DG : GB = 1 : 8 $.

Notes : For a more effective way to work on example question number 5, we can use Menelaus' theorem. The method is:

  • Determine the comparison $ EG : GC $ : $$\begin{align*} \frac{EG}{GC}.\frac{CD}{DA}.\frac{AB}{EB} &= 1\\\frac{EG}{GC}.\frac{1}{3}.\frac{3}{2} &= 1\\\frac{EG}{GC}.\frac{1}{2} &= 1\\\frac{EG}{GC}&= 1 : \frac{1}{2} \\\frac{EG}{GC}&= \frac{2}{1} \end{align*}$$
  • Determine the ratio $ DG : GB $ : $$\begin{align*} \frac{DG}{GB}.\frac{BE}{EA}.\frac{AC}{CD} &= 1\\\frac{DG}{GB}.\frac{2}{1}.\frac{4}{1} &= 1\\\frac{DG}{GB}.\frac{8}{1}&= 1\\\frac{DG}{GB} &= 1 : \frac{8}{1}\\\frac{DG}{GB} &= \frac{1}{8} \end{align*}$$

How is the result? Yup, it’s the same as using Menelaus' theorem.

Exercise 5

  1. Given the points P(1, 7) and Q(4, 1). Point R is a point on the line PQ, such that $\overset{\to }{\mathop{PR}}=\frac{1}{3}\overset{\to }{\mathop{PQ}}$. Determine the coordinates of point R.