Comparative Values ​​Of Trigonometry in Various Quadrants

Determining Trigonometric Comparison Values ​​of Sine, Cosine, Tangent in Quadrant I, Quadrant II, Quadrant III, Quadrant IV

This time we will discuss trigonometry comparisons in various quadrants. Previously, we learned about determining the trigonometric ratio values ​​of acute angles in right triangles. Read Trigonometric Comparisons in Right Triangles↝ and Special Angle Trigonometric Comparisons↝ . This concept can be extended to a wide range of angles. Of course, the values ​​and signs at each angle are different. some are positive and some are negative.

At junior high school level we already know about Cartesian coordinates. The coordinate axes divide the coordinate plane into four regions referred to as quadrants. Based on this, the angles in a Cartesian coordinate can be divided into 4 areas which are divided into quadrant I, quadrant II, quadrant III and quadrant IV. So, next, let’s discuss trigonometry comparison values ​​in various quadrants.

Trigonometry Comparison Values ​​in Various Quadrants

We know that in one revolution the angle is $360^\circ$. As rotation angles, angles are grouped into four regions or quadrants based on magnitude angle, namely:

1. Quadrant I: with angles $0^\circ$ to $90^\circ$ or $0 < x < \frac{\pi}{2}$
2. Quadrant II: with angles $90^\circ$ to $180^\circ$ or $\frac{\pi}{2} < x < \pi$
3. Quadrant III: with angles $180^\circ$ to $270^\circ$ or $\pi < x < \frac{3\pi}{2}$
4. Quadrant IV: with angles $270^\circ$ to $360^\circ$ or $\frac{3\pi}{2} < x < 2\pi$

with a value of $\pi = 180^\circ$ for the angle. Apart from angles in various quadrants, there are also angles greater than $360^\circ$ and also negative angles.

The trigonometry comparison values ​​are as shown in the following image.

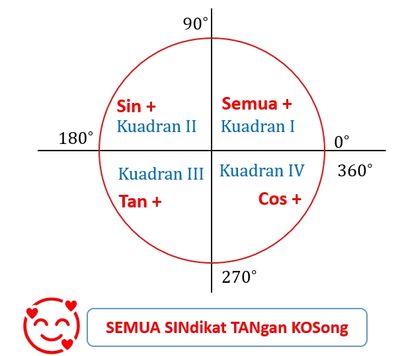
From the image above it is obtained,

1. Quadrant I, all trigonometric comparison values ​​are positive (sin, cos, tan, sec, csc, cot)
2. Quadrant II, value sin is positive (so is csc) other values ​​are negative (cos, tan, sec, cot)
3. Quadrant III, tan is positive (so is cot) other values ​​are negative (sin, cos, sec, csc)
4. Quadrant IV, cos is positive (so is sec) other values ​​are negative (sin, tan, csc, cot).

To make it easier to remember, use the words “ALL EMPTY HANDED SYNDICATES”.

Problems example

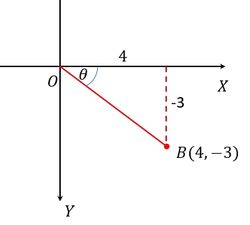
1. Given point B(4,-3) if $\angle XOB=\theta$ determine the value of $\sin \theta, \cos\theta, \tan\theta$ !

   Solution ✍️

   By drawing point B in Cartesian coordinates, it is clear that point B is in quadrant IV.

   From the picture, it can be seen that XB or the length of the front side is $y=3$, and OX or the length of the side side is $x=4$. Next, we find the length of OB or hypotenuse using Pythagoras. $$\begin{align*} OB&=\sqrt{x^2+y^2}\\ &=\sqrt{4^2+3^2}\\ &=\sqrt{16+9}\\ &=\sqrt{25}\\ OB&=5 \end{align*}$$ Obtain the length of the hypotenuse or OB=5.

   • Determine trigonometric comparison values $$\begin{align*}\sin \theta & = \frac{de}{mi} = \frac{-3}{5}=-\frac{3}{5} \\\cos \theta & = \frac{sa}{mi} = \frac{4}{5} \\\tan \theta & = \frac{de}{sa} = \frac{-3}{4} = - \ frac{3}{4} \end{align*}$$

   Note: in quadrant IV, cos is (+), while sin and tan are (-)

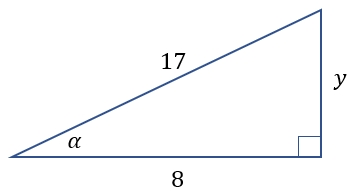
2. Know the value of $\cos \alpha = -\dfrac{8}{17}$ with $\alpha$ in quadrant II. Determine the value of $\sin \alpha ,$ and the value of $\tan \alpha$?

   Solution ✍️

   • Draw a right triangle to make it easier. value $\cos \alpha = -\dfrac{8}{17} \rightarrow \dfrac{sa}{mi} = \dfrac{-8}{17},$ means side 8 (temporarily ignore the - sign) and side slant 17, so first find the front side using the Pythagorean theorem. let the front side $y$ then $$y=\sqrt{17^2-8^2}=\sqrt{289-64}=\sqrt{225}=15$$ Obtained front side 15.
   • Because $\alpha$ is in quadrant II, the value of sin is positive and tan is negative. $$\begin{align*} \sin \alpha &= \frac{de}{mi} = \frac{15}{17} \\ \tan \alpha &= \frac{de}{sa} = - \frac{15}{8} \end{align*}$$

   So, $\sin \alpha = \frac{15}{17} ,$ and $\tan \alpha = - \frac{15}{8}$ are obtained.