The area of a triangle can be calculated using the formula base area times height divided by two. Apart from that, you can also use the rules of trigonometry
The area of a triangle that we previously understood was calculated using the formula base area times height divided by two or can be written $$ L\triangle=\frac12\times a \times t$$
Apart from using the formula above, the area of the triangle can also be obtained using trigonometry formulas. But first, please study Trigonometric Comparisons in Right Triangles↝ , Special Angle Trigonometric Comparisons↝ , and also [Sine Rule and Cosine](/sine-and-cosine-trigonometry rules) to understand more about trigonometry.
Area of a Triangle with Trigonometry Rules
1. Area of a Triangle if two sides and one angle are known
Look at the following triangle ABC with its angles and sides!
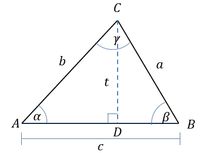
The area of triangle ABC is: $$\begin{align} L \triangle ABC &= \frac12 \times \text{alas} \times \text{tinggi}\nonumber\\ &= \frac12 \times c \times t \end{align}$$ Note that the triangle ADC, with trigonometric ratios is obtained $$\sin\alpha=\frac{t}{b}$$ atau $$\begin{align}t=b\sin\alpha\end{align}$$ From press (1) and press (2), then $$\begin{align}L \triangle ABC &= \frac12\times c \times t\nonumber\\ &= \frac12 \times c \times b \sin\alpha \nonumber\\ L \triangle ABC &= \frac{1}{2}bc\sin\alpha \end{align}$$ In the same way, for each triangle ABC also applies:
$$\begin{align*} L \triangle ABC &= \frac{1}{2}bc\sin\alpha \\ L \triangle ABC &= \frac{1}{2}ac\sin\beta \\ L \triangle ABC &= \frac{1}{2}ab\sin\gamma \end{align*}$$
Problems example
Determine the area of triangle ABC if side $BC=4$ cm, $AC=7\sqrt3$ cm and $\angle C=60\degree$.
Solution ✍️
$BC=4$ cm, $AC=7\sqrt3$ cm dan $\angle C=60\degree$
By using the triangle area formula, trigonometry rules $$\begin{align*}L \triangle ABC &= \frac{1}{2}BC.AC.\sin C \\ &= \frac{1}{2}(4)(7\sqrt3)\sin 60\degree \\ &= \frac{1}{2}(4)(7\sqrt3)\frac12\sqrt3 \\ &= \frac{1}{4}(4)(7\sqrt3)(\sqrt3) \\ &= (7)(3) \\&= 21 \end{align*}$$ So, the area of triangle ABC is $21 \text{ cm}^2$.
2. Area of a Triangle if all three sides are known
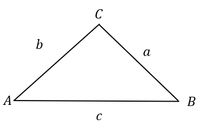The area of triangle ABC is $$ L = \sqrt{s(s-a)(s-b)(s-c)} $$
with $ s = \dfrac{1}{2}(a+b+c) $ or $ s = \dfrac{1}{2} \times \text{ (perimeter of triangle ABC)} $Proof of Heron’s formula
- In triangle ABC the Cosine rule for angle A applies $$\begin{align*}a^2 = b^2 + c^2 - 2bc \cos A \\ \rightarrow \cos A = \frac{b^2 + c^2 - a^2 }{2bc}\tag{1} \end{align*}$$
- Identitas Trigonometri: $$ \sin ^2 A + \cos ^2 A = 1 \\ \rightarrow \sin ^2 A = 1 - \cos ^2 A \\ \rightarrow \sin ^2 A = (1-\cos A)(1+\cos A) \tag{2}$$
- Substitute press (1) into press (2)
$$ \begin{align*}\sin ^2 A &= 1 - \cos ^2 A \\\sin ^2 A &= (1 - \cos A )(1 + \cos A )\\ &= \left(1 - \frac{b^2 + c^2 - a^2 }{2bc} \right) \left(1 + \frac{b^2 + c^2 - a^2 }{2bc} \right)\\ &= \left( \frac{2bc - b^2 - c^2 + a^2 }{2bc} \right) \left( \frac{2bc + b^2 + c^2 - a^2 }{2bc} \right)\\ &= \left( \frac{-(b-c)^2 + a^2 }{2bc} \right) \left( \frac{(b+c)^2- a^2}{2bc} \right)\\ &= \left( \frac{ a^2 -(b-c)^2 }{2bc} \right) \left( \frac{(b+c)^2- a^2 }{2bc} \right)\\ &= \left( \frac{ (a-b+c)(a+b-c) }{2bc} \right) \left( \frac{(b+c-a)(b+c+a) }{2bc} \right)\\ \sin ^2 A &= \frac{ (a-b+c)(a+b-c)(b+c-a)(b+c+a) }{(2bc)(2bc)} \\ \sin A &= \sqrt{ \frac{ (a-b+c)(a+b-c)(b+c-a)(b+c+a) }{(2bc)(2bc)} } \\ \sin A &= \frac{1}{2bc}\sqrt{ (a-b+c)(a+b-c)(b+c-a)(b+c+a) } \end{align*} $$
for example : $ s = \frac{1}{2}(a+b+c) $ therefore
- $2s=a+b+c$
- $b+c-a=(a+b+c)-2a=2s-2a=2(s-a)$
- $a+c-b=(a+b+c)-2b=2s-2b=2(s-b)$
- $a+b-c=(a+b+c)-2c=2s-2c=2(s-c)$
until obtained $$\begin{align*} \sin A &= \frac{1}{2bc}\sqrt{ (a-b+c)(a+b-c)(b+c-a)(b+c+a) }\\ &= \frac{1}{2bc}\sqrt{ 2s\cdot2(s-a)\cdot2(s-b)\cdot2(s-c) }\\ A &= \frac{1}{2bc}\sqrt{ 16s(s-a)(s-b)(s-c) }\\ A &= \frac{4}{2bc}\sqrt{ s(s-a)(s-b)(s-c) }\\ \sin A &= \frac{2}{bc}\sqrt{ s(s-a)(s-b)(s-c) } \end{align*}$$
Area of triangle ABC using angle A: $$ \begin{align*}L &= \frac{1}{2}.AB.AC. \sin A\\ &= \frac{1}{2}.c.b. \frac{2}{bc}\sqrt{ s (s-a)(s-b)(s-c) }\\ &= \sqrt{ s (s-a)(s-b)(s-c) } \end{align*} $$ So, the area of the triangle is proven.
Problems example
Determine the area of triangle ABC if it is known that the sides $a=13$ cm, $b=14$ cm and $c=15$ cm.
Solution ✍️
$a=13$ cm, $b=14$ cm dan $c=15$ cm.$$\begin{align*}s&=\frac12(a+b+c)\\ &=\frac12(13+14+15) \\ &= 21 \end{align*}$$ Use the triangle area formula if the number of sides is known $$ \begin{align*}L\triangle ABC &= \sqrt{ s (s-a)(s-b)(s-c) } \\ &= \sqrt{ 21 (21-13)(21-14)(21-15) } \\ &= \sqrt{ 21 (8)(7)(6) } \\ &= \sqrt{ 7056 } \\ &= 84 \end{align*} $$
So, the area of triangle ABC is $84 \text{ cm}^2$.