In this article we will discuss several applications of vectors, namely Resultant Vectors, Normal Vectors, Orthogonal Projections of Vectors, Distance from point to line, and Area and Volume.
In this article we will discuss several applications of vectors, namely Resultant Vectors, Normal Vectors, Orthogonal Projections of Vectors, Distance from point to line, and Area and Volume.
1. Result of Two Vectors
Look at the image on the side below.
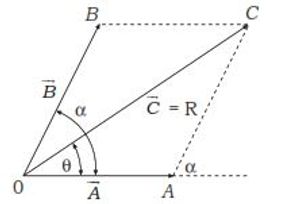Given two vectors, namely vectors $\vec{a}$ and $\vec{b}$ and the angle formed by vector $\vec{b}$ with respect to vector $\vec{a}$, namely $\alpha $. The resultant of the vectors $\vec{a}$ and $\vec{b}$ is the same as finding the length of OC.
Using the triangle rule, we can find the length of OC in the following way. $$\left| \overrightarrow{OC} \right|^{2}={{\left| \overrightarrow{OA} \right|}^{2}}+{{\left| \overrightarrow{AC} \right|}^{2}}+2\left| \overrightarrow{OA} \right|\left| \overrightarrow{AC} \right|\cos \alpha $$ Thus the resultant of two vectors $\vec{a}$ and $\vec{b}$ is: $$R=\sqrt{{{\left| \overrightarrow{a} \right|}^{2}}+{{\left| \overrightarrow{b} \right|}^{2}}+2\left| \overrightarrow{a} \right|\left| \overrightarrow{b} \right|\cos \alpha }$$ Furthermore, if the resultant of vectors $\vec{a}$ and $\vec{b}$, namely vector $\vec{r}$ forms an angle θ with respect to vector $\vec{a}$ then the direction of the resultant vector R can be found with the following formula. $$\sin \theta =\frac{\left| \vec{b} \right|\sin \alpha }{R}$$
Example:
A ship is stuck in the middle of the sea. To bring the ship back to port two tugboats are needed. The force required by the two ships and the angle formed can be seen in the picture on the side. Determine the magnitude of the resultant force produced by the two ships!
Alternative Solutions:
The resultant forces of the two ships are depicted in the force diagram on the side.
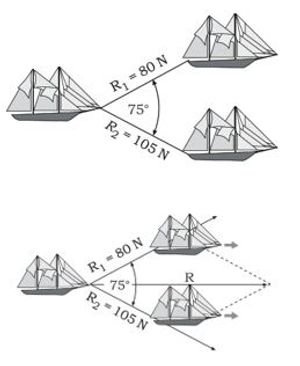The resultant forces for both ships are given as follows.
$$\begin{align*} & R=\sqrt{R_1^2+R_2^2+2R_1R_2\cos \alpha } \\ & R=\sqrt{{{80}^{2}}+{{105}^{2}}+2\cdot 80\cdot 105\cos 75{}^\circ } \\ & R\approx \sqrt{6.400+11.025+16.800\cdot 0,26} \\ & R\approx \sqrt{6.400+11.025+4.368} \\ & R\approx \sqrt{21.793} \\ & R\approx 147,62 \end{align*}$$
So, the resultant force on both ships is 147.62 N.
2. Straight Line Normal Vector in R2 and Plane Normal in R3
The normal vector of a line is a vector that is perpendicular to that line. Because the condition is that it is perpendicular, the normal vector can be long or short, as long as it is not a zero vector. Usually the normal vector chosen is the simplest normal vector.
Theorem
$\vec{n}=\left( \begin{matrix} a \\ b \end{matrix} \right)\text{ perpendicular to the line }ax+by+c=0$ in two-dimensional space R2
$\vec{n}=\left( \begin{matrix} a \\ b \\ c \end{matrix} \right)\text{ perpendicular to line }ax+by+cz+d=0 $ in three-dimensional space R3
3. Orthogonal Projection of a Vector to Another Vector
Orthogonal projection of a vector onto another vector, the result is a vector. Meanwhile, the length of the projection of an orthogonal vector on another vector is always a positive real number/scalar.
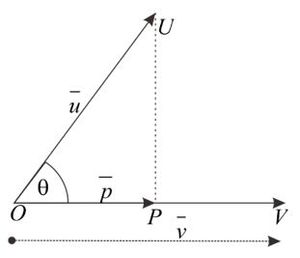The orthogonal projection of vector $\vec{u}$ on vector $\vec{v}$ can be denoted by ${\vec{u}}_{\vec{v}}$ or $\vec{p}$ and is defined by the following argument.
Proposition:
- Scalar Projection orthogonal $\vec{u}$ falls on $\vec{v}$ is $$\left| \left| \vec{p}\right| \right|=\frac{\vec{u}\cdot\vec{v}}{\left| \vec{v} \right|}$$
- The projection of the vector $\vec{u}$ onto the vector $\vec{v}$ is the vector $${\vec{u}}_{\vec{v}}=\left( \frac{\vec{u } \cdot \vec{v}}{\left|. \vec{v} \right|^2} \right)\vec{v}\text{ atau } \vec{p}=\frac{\vec{u }}{\left| \vec{v} \right|} \left| \left| \vec{p} \right| \right|$$
- Panjang project vector $\vec{u}$ to vector $\vec{v}$ is $$ \lvert \vec{u}_{\vec{v}}\rvert=\left| \vec{u}\cdot e_{\vec{v}} \right| $$ dengan $e_{\vec{v}}$ is vector satuan ke arah $\vec{v}$ atau $\left| \vec{u}_{\vec{v}} \right|=\left| \frac{\vec{u}.\vec{v}}{\left| \vec{v} \right|} \right|$ .
Example 1:
Given $\vec{a}=2\widehat{i}-6\widehat{j}-3\widehat{k}$ and $\vec{b}=4\widehat{i}+2\widehat{j} -4\widehat{k}$. Determine:
- The length of the vector projection $\vec{a}$ on $\vec{b}$
- Orthogonal projection of vector $\vec{a}$ on $\vec{b}$
- Orthogonal projection of vector $\vec{b}$ on $\vec{a}$
Alternative Solutions:
The length of the vector projection $\vec{a}$ on $\vec{b}$ $$\begin{align*} \left| \vec{a}_{\vec{b}} \right|=\left| \frac{\vec{a}.\vec{b}}{\left| \vec{b} \right|} \right|&=\left| \frac{(2\widehat{i}-6\widehat{j}-3\widehat{k})\cdot (4\widehat{i}+2\widehat{j}-4\widehat{k})}{\sqrt{{{4}^{2}}+{{2}^{2}}+{{(-4)}^{2}}}} \right| \\ &=\left| \frac{(2)(4)+(-6)(2)+(-3)(-4)}{\sqrt{16+4+16}} \right| \\ &=\left| \frac{8-12+12}{\sqrt{36}} \right|=\left| \frac{8}{6} \right| \end{align*}$$ $ \therefore \left| \vec{a}_{\vec{b}} \right|=\frac{4}{3}$
Orthogonal projection of vector $\vec{a}$ on $\vec{b}$
$\vec{a}_{\vec{b}}=\left| \left| \vec{a}_{\vec{b}} \right| \right|\frac{\vec{b}}{\left| \vec{b} \right|}$, karena $\left| \vec{b} \right|=6$ dan $\left| \left| {{\vec{a}}_{\vec{b}}} \right| \right|=\frac{4}{3}$
$$\begin{align*} \vec{a}_{\vec{b}}&=\frac{4}{3}.\frac{4\widehat{i}+2\widehat{j}-4\widehat{k}}{6} \\ & =\frac{8}{9}\widehat{i}+\frac{4}{9}\widehat{j}-\frac{8}{9}\widehat{k} \end{align*}$$Orthogonal projection of vector $\vec{b}$ on $\vec{a}$
$$\begin{align*}\vec{b}_{\vec{a}}&=\left( \frac{\vec{b}\cdot \vec{a}}{{{\left| \vec{a} \right|}^{2}}} \right)\vec{a} \\ &=\frac{(4\widehat{i}+2\widehat{j}-4\widehat{k})\cdot (2\widehat{i}-6\widehat{j}-3\widehat{k})}{{{\left( \sqrt{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}} \right)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{(4)(2)+(2)(-6)+(-4)(-3)}{{{2}^{2}}+{{(-6)}^{2}}+{{(-3)}^{2}}}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ &=\frac{8}{49}(2\widehat{i}-6\widehat{j}-3\widehat{k}) \\ \vec{b}_{\vec{a}}&=\frac{16}{49}\widehat{i}-\frac{48}{49}\widehat{j}-\frac{24}{49}\widehat{k})\end{align*}$$
4. The point-to-line distance in R2 and the point-to-plane distance in R3
Proposition:
In two-dimensional space (R2), the distance of the point $P(x_1,y_1)$ to the line $ax+by+c=0$ is $$d=\left| \frac{ax_1+by_1+c}{\sqrt{a^2+b^2}} \right|$$
On the three-dimensional space (R3) , the distance of the point $P(x_1,y_1,z_1)$ to the line $ax+by+cz+d=0$ is $$d=\left| \frac{ax_1+by_1+cz_1+d}{\sqrt{a^2+b^2+c^2}} \right|$$
Example
Determine the distance from point (7,1) to the line 4x –3y +10 = 0!
Alternative Solution
- Vector way
Normal garis g : 4x-3y+10 = 0 is $\vec{n}=\left( \begin{matrix}4\\-3 \end{matrix} \right)$
Choose a point on the line $4x-3y+10 = 0$ which has round coordinates, for example $(–1 ,2)$. $$\vec{u}=\left( \begin{matrix}7 \\ 1 \end{matrix} \right)-\left( \begin{matrix} -1 \\ 2\end{matrix} \right)=\left( \begin{matrix} 8 \\ -1 \end{matrix} \right)$$ The distance from the point to the line in question is: $$\begin{align*}& d=\left| \frac{\vec{u}.\vec{n}}{\left| \vec{n} \right|} \right| \\ & d=\left| \frac{\left( \begin{matrix} 8 \\ -1 \end{matrix} \right)\left( \begin{matrix} 4 \\ -3 \end{matrix} \right)}{\sqrt{4^2+(-3)^2}} \right|=\left| \frac{32+3}{5} \right|=7 \end{align*}$$ - Analytical way
$$\begin{align*} & d=\left| \frac{ax_1+by_1+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|= \\ & d=\left| \frac{(4)(7)-3(1)+10}{\sqrt{4^2+3^2}} \right| \\ & d=\left| \frac{28-3+10}{\sqrt{25}} \right|=\frac{35}{5} \\ & d=7\end{align*}$$
5. Surface area and volume of a geometric shape
The area of the parallelogram formed by vector $\vec{u}$ and vector $\vec{v}$ is $$\begin{align*} & L=\text{alas }\times \text{ tinggi} \\ & L=\left| \vec{u} \right|\left| \vec{v}\sin \theta \right| \\ & L=\left| \vec{u} \right|\left| \vec{v} \right|\sin \theta ,\text{ }0\le \theta \le 180 \end{align*}$$ Because the value $\sin \theta $ is always positive then $L=\left| \vec{u} \right|\left| \vec{v} \right|\sin \theta $ can also be written $L=\left| \vec{u}\times \vec{v} \right|$.
Since the area of the triangle is exactly $\dfrac12$ of the parallelogram area, the area of the triangle is: ${{L}_{\vartriangle }}=\frac{1}{2}\left| \vec{u}\times \vec{v} \right|$
A parallel epipedum is a 6-sided space object whose parallel sides are congruent and each side is a parallelogram. The volume of the parallel epipedum formed by 3 vectors $\vec{u},\text{ }\vec{v},$ and $\vec{w}$ is: $$V=\left| \vec{u}\cdot (\vec{v}\times \vec{w}) \right|=\left| \vec{v}\cdot (\vec{u}\times \vec{w}) \right|=\left| \vec{w}\cdot (\vec{u}\times \vec{v}) \right|$$
Example:
It is known that block ABCD EFGH with AB = 6, BC = 5, and CG = 4 is located in space coordinates R3 as shown in the figure. Determine the area of the ACH field!
Alternative Solutio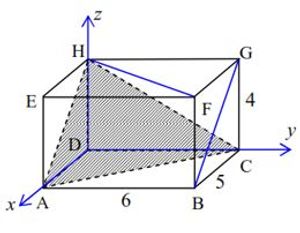n
From the image provided we can state that the coordinates of point A(5, 0, 0) ; B(5, 6, 0) ; C(0, 6, 0) ; H(0, 0, 4) ; F(5, 6, 4) ; and G(0, 6, 4). From this data, the area of the ACH field
$$\begin{align*} & L=\frac{1}{2}\left| \overrightarrow{AC}\times \overrightarrow{AH} \right| \\ & L=\frac{1}{2}\left| (\vec{c}-\vec{a})\times (\vec{h}-\vec{a}) \right| \\ & L=\frac{1}{2}\left| \left( \begin{matrix} -5 \\ 6 \\0 \end{matrix} \right)\times \left( \begin{matrix} -5 \\ 0 \\ 4 \end{matrix} \right) \right|=\frac{1}{2}\left| \left( \begin{matrix} \left| \begin{matrix} 6 & 0 \\ 0 & 4 \end{matrix} \right| \\ \left| \begin{matrix}0 & 4 \\ -5 & -5 \end{matrix} \right| \\ \left| \begin{matrix}-5 & -5 \\ 6 & 0 \end{matrix} \right| \end{matrix} \right) \right|=\frac{1}{2}\left| \begin{matrix} 24 \\ 20 \\ 30 \end{matrix} \right| \\ & L=\left| \begin{matrix} 12 \\ 10 \\ 15 \end{matrix} \right|=\sqrt{{{12}^{2}}+{{10}^{2}}+{{15}^{2}}}=\sqrt{469}\approx 21,66 \end{align*}$$